 por barbara-rabello » Dom Out 06, 2013 18:58
por barbara-rabello » Dom Out 06, 2013 18:58
Boa tarde! Estou estudando critérios de divisibilidade e congruências e me deparei com o seguinte problema:
Preciso encontrar o resto da divisão de
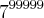
por 100.
Um professor me ajudando, me falou que era assim:
Como 99999 = 4.24444 + 3 e
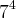

1 mod 100, temos que
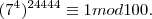
Portanto,
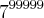
=

.
Não conseguir entender esta solução para o problema. Alguém pode me ajudar?
-
barbara-rabello
- Usuário Dedicado

-
- Mensagens: 49
- Registrado em: Sex Mar 02, 2012 16:52
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: cursando
 por matmatco » Dom Dez 08, 2013 22:44
por matmatco » Dom Dez 08, 2013 22:44
ele apenas reescreveu 99999 como 4.24444 + 3 mas isto está errado na verdade 99999= 4.2499+ 3 com isso usando congruência vemos que

logo reescrevendo temos

e sabendo que

temos
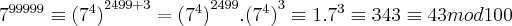
.
espero ter ajudado abraços
-
matmatco
- Usuário Parceiro

-
- Mensagens: 60
- Registrado em: Qua Ago 24, 2011 17:32
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica UFV
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- algebra l
por ehrefundini » Qui Mar 05, 2009 08:34
- 1 Respostas
- 7464 Exibições
- Última mensagem por Molina

Qui Mar 05, 2009 21:50
Álgebra
-
- algebra
por uspsilva » Sex Mar 13, 2009 13:03
- 1 Respostas
- 3209 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 15:22
Pedidos
-
- Algebra
por mattheusramos14 » Ter Ago 03, 2010 01:26
- 1 Respostas
- 2738 Exibições
- Última mensagem por MarceloFantini

Ter Ago 03, 2010 13:37
Álgebra Elementar
-
- ALGEBRA
por JOHNY » Sex Set 03, 2010 23:50
- 1 Respostas
- 2709 Exibições
- Última mensagem por MarceloFantini

Sáb Set 04, 2010 13:12
Álgebra Elementar
-
- álgebra
por Eliana Fidelis » Dom Out 24, 2010 13:52
- 1 Respostas
- 2650 Exibições
- Última mensagem por Adriano Tavares

Ter Mar 08, 2011 20:37
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
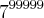 por 100.
por 100.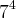
 1 mod 100, temos que
1 mod 100, temos que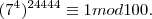
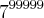 =
=  .
.
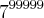 por 100.
por 100.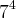
 1 mod 100, temos que
1 mod 100, temos que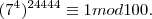
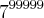 =
=  .
.
 logo reescrevendo temos
logo reescrevendo temos  e sabendo que
e sabendo que  temos
temos 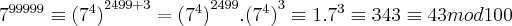 .
.