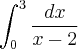
Separei em 2 integrais

Aplicando os Limites nas 2, e através do Principio de Calculo, chego a
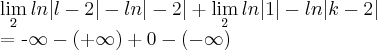
=

Ou seja, diverge... Está correta a resolução?

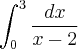

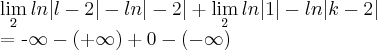


dehcalegari escreveu:Calcular
Separei em 2 integrais
Aplicando os Limites nas 2, e através do Principio de Calculo, chego a
=
Ou seja, diverge... Está correta a resolução?








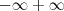 , então fazemos o seguinte :
, então fazemos o seguinte :

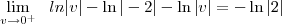 , esse resultado é conhecido como Valor Principal de Cauchy.
, esse resultado é conhecido como Valor Principal de Cauchy.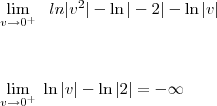

Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes

 .
.



