 por ravi » Qui Set 19, 2013 15:36
por ravi » Qui Set 19, 2013 15:36
Boa tarde, tentei resolver essa questão que foi de uma prova que fiz, mas não consegui muito coisa.
Seja R uma região plana limitada pelas curvas y=f(x) e y=g(x) inteiramente contida de um lado do eixo y. Mostre que se R é girada ao redor do eixo y, então o volume do sólido resultante é o produto da área A de R e a distância d percorrida pelo centróide de R.
-
ravi
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Jan 31, 2012 13:20
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por young_jedi » Sex Set 20, 2013 21:39
por young_jedi » Sex Set 20, 2013 21:39
o centroide de R tem coordenadas dadas por

a fazer um giro em torno de y temos que o caminho que ele percorre sera

temos que
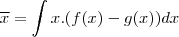
e temos que o volume do solido obtido pela rotação


ou seja
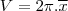
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Uma questao complicada pra mim ;/
por hian » Dom Nov 14, 2010 16:50
- 1 Respostas
- 1625 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:33
Binômio de Newton
-
- Questão Complicada
por Kelvin Brayan » Dom Abr 24, 2011 11:01
- 2 Respostas
- 2886 Exibições
- Última mensagem por Kelvin Brayan

Dom Abr 24, 2011 15:01
Sistemas de Equações
-
- [questão complicada]
por JKS » Qui Jun 20, 2013 01:48
- 1 Respostas
- 2456 Exibições
- Última mensagem por adauto martins

Seg Jan 05, 2015 16:24
Números Complexos
-
- Função implícita; Questão complicada!
por jemourafer » Qui Mai 17, 2012 18:30
- 4 Respostas
- 4244 Exibições
- Última mensagem por Fabio Wanderley

Sáb Mai 19, 2012 03:16
Cálculo: Limites, Derivadas e Integrais
-
- Questão prova concurso (volume)
por fernandocez » Qui Mar 24, 2011 11:54
- 4 Respostas
- 3705 Exibições
- Última mensagem por fernandocez

Qui Mar 24, 2011 18:51
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




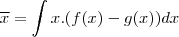


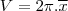



 , avisa que eu resolvo.
, avisa que eu resolvo.

