Se a área do triângulo retângulo é 3n, sendo a altura dada por:
 , eixo das ordenadas e a base do triângulo ser n eixo das absissas , concluí-se que f(n) é igual a:
, eixo das ordenadas e a base do triângulo ser n eixo das absissas , concluí-se que f(n) é igual a: , daqui eu não sei sair.
, daqui eu não sei sair.
 , eixo das ordenadas e a base do triângulo ser n eixo das absissas , concluí-se que f(n) é igual a:
, eixo das ordenadas e a base do triângulo ser n eixo das absissas , concluí-se que f(n) é igual a: , daqui eu não sei sair.
, daqui eu não sei sair.
 , ou seja,
, ou seja,  e, daí:
e, daí: 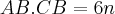 . Ainda temos que a base é dada por
. Ainda temos que a base é dada por  e a altura é dada por uma função,
e a altura é dada por uma função,  . Tudo isto nos diz que: a área é um número fixo e a base também, porém a altura pode variar conforme o valor de x. Por outro lado, note que se o exercício pede o valor de
. Tudo isto nos diz que: a área é um número fixo e a base também, porém a altura pode variar conforme o valor de x. Por outro lado, note que se o exercício pede o valor de  , então está pedindo o valor que a função assume quando
, então está pedindo o valor que a função assume quando  , ou seja, está querendo o valor de
, ou seja, está querendo o valor de  , que você já encontrou. Para ficar mais claro, veja que se substituir o valor 6 encontrado, você obtém a área, que já foi dada. Assim:
, que você já encontrou. Para ficar mais claro, veja que se substituir o valor 6 encontrado, você obtém a área, que já foi dada. Assim: 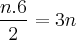 . Então:
. Então:  .
.



![2\sqrt[]{2} 2\sqrt[]{2}](/latexrender/pictures/202687598843121ee5b0808a42feb662.png) , 3 ,
, 3 ,![3\sqrt[]{3} 3\sqrt[]{3}](/latexrender/pictures/8f02447859000765689bdee72a9b79b7.png) e 4.
e 4.



Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante