 por lucasdemirand » Dom Ago 25, 2013 11:56
por lucasdemirand » Dom Ago 25, 2013 11:56
olá amigos, estou com uma duvida para a realização do seguinte problema,
encontre a derivada de :
![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)
-
lucasdemirand
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Sáb Jul 06, 2013 12:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecanica
- Andamento: cursando
 por Pessoa Estranha » Dom Ago 25, 2013 14:49
por Pessoa Estranha » Dom Ago 25, 2013 14:49
lucasdemirand escreveu:olá amigos, estou com uma duvida para a realização do seguinte problema,
encontre a derivada de :
![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)
Olha, você pode pensar assim:
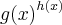
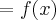
, onde

e
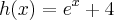
.
Daí, antes de passarmos para a fórmula, pensemos um pouco: observe que tomando

(apenas para facilitar), vem que:
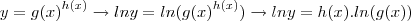
.
Então:
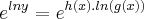
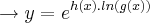
Ou seja:
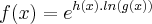
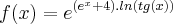
Derivando:
![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´ f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´](/latexrender/pictures/2ca4a017cae58d3efc36824e894b899b.png)
Aí, basta aplicar regra da derivada do produto:
![(({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]= (({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]=](/latexrender/pictures/8d8f1b8c99d6015324f1b9d9ee5f0938.png)
![=[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] =[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/390a4c444ede1456b17404d3bba85acd.png)
![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/d0a4d51ee68e79dfb9c0535340683493.png)
Por favor, desconsidere estes "Â" (ainda não sei o motivo pelo qual aparecem).
Espero que esteja certo. Você tem a resposta? Se sim, coloque aqui.
O que eu fiz foi usar as funções logaritmo na base

e a exponencial também de base

, pois uma é o inverso da outra. Depois, concluindo, apliquei o restante da fórmula de derivada de função composta. Pode ser que, às vezes, eu acabe errando em alguma conta, mas a ideia é esta.
Espero ter ajudado.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivada] Ajuda com calculo de derivada de função quociente
por alienpuke » Dom Out 25, 2015 15:31
- 1 Respostas
- 12556 Exibições
- Última mensagem por Cleyson007

Dom Out 25, 2015 16:47
Cálculo: Limites, Derivadas e Integrais
-
- [derivada] derivada pela definição da secante
por TheKyabu » Sáb Out 27, 2012 23:24
- 2 Respostas
- 10888 Exibições
- Última mensagem por TheKyabu

Dom Out 28, 2012 11:44
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada] Com duas variáveis e derivada mista
por leticiaeverson » Dom Abr 22, 2018 00:39
- 3 Respostas
- 13193 Exibições
- Última mensagem por Gebe

Dom Abr 22, 2018 17:11
Cálculo: Limites, Derivadas e Integrais
-
- [Derivada]derivada de função de raiz cúbica
por armando » Sáb Jul 20, 2013 15:22
- 4 Respostas
- 14798 Exibições
- Última mensagem por armando

Dom Jul 21, 2013 22:17
Cálculo: Limites, Derivadas e Integrais
-
- [DERIVADA] DERIVADA POR DEFINIÇÃO DA RAIZ DO MÓDULO DE X
por Matheusgdp » Qua Set 16, 2015 04:07
- 2 Respostas
- 5115 Exibições
- Última mensagem por Matheusgdp

Qui Set 17, 2015 18:31
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)

![f(x)= {\left[tg(x) \right]}^{{e}^{x}+4} f(x)= {\left[tg(x) \right]}^{{e}^{x}+4}](/latexrender/pictures/5b3a5910517da99b8b8e487852c1a26a.png)

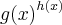
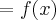 , onde
, onde  e
e 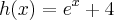 .
. (apenas para facilitar), vem que:
(apenas para facilitar), vem que: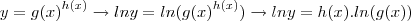 .
.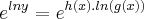
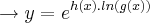
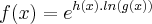
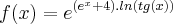
![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´ f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}+4).ln(tg(x))]´](/latexrender/pictures/2ca4a017cae58d3efc36824e894b899b.png)
![(({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]= (({e}^{x}+4).ln(tg(x))´= [({e}^{x}+4)´.ln(tg(x))]+[ln(tg(x)).({e}^{x}+4)]=](/latexrender/pictures/8d8f1b8c99d6015324f1b9d9ee5f0938.png)
![=[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] =[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/390a4c444ede1456b17404d3bba85acd.png)
![f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)] f´(x)={e}^{({e}^{x}+4).ln(tg(x))}.[({e}^{x}).ln(tg(x))]+[\frac{cosx}{senx}.({e}^{x}+4)]](/latexrender/pictures/d0a4d51ee68e79dfb9c0535340683493.png)
 e a exponencial também de base
e a exponencial também de base  , pois uma é o inverso da outra. Depois, concluindo, apliquei o restante da fórmula de derivada de função composta. Pode ser que, às vezes, eu acabe errando em alguma conta, mas a ideia é esta.
, pois uma é o inverso da outra. Depois, concluindo, apliquei o restante da fórmula de derivada de função composta. Pode ser que, às vezes, eu acabe errando em alguma conta, mas a ideia é esta.


 substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
substitui-se m, substitui-se y e x por um dos pares ordenados, e resolve-se em ordem a b.
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.