Considere o grupo aditivo
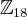 e
e 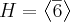 e
e 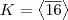 . Mostre que
. Mostre que  é um subgrupo cíclico de
é um subgrupo cíclico de 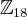 gerado por
gerado por  .
.Se alguém souber, agradeço.

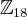 e
e 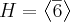 e
e 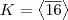 . Mostre que
. Mostre que  é um subgrupo cíclico de
é um subgrupo cíclico de 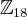 gerado por
gerado por  .
.
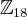 ???
???
Cleyson007 escreveu:Boa noite!
Considere o grupo aditivoe
e
. Mostre que
é um subgrupo cíclico de
gerado por
.
Se alguém souber, agradeço.
 é um subgrupo (se precisar, é fácil demonstrar). O subgrupo H é formado por
é um subgrupo (se precisar, é fácil demonstrar). O subgrupo H é formado por  e o subgrupo K é formado por
e o subgrupo K é formado por  portanto a interseção
portanto a interseção 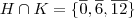 o que é um subgrupo (como afirmei anteriormente) cíclico (veja que, aplicando sucessivamente a operação do grupo a classe 12 as classes do subgrupo
o que é um subgrupo (como afirmei anteriormente) cíclico (veja que, aplicando sucessivamente a operação do grupo a classe 12 as classes do subgrupo  se repetirão) gerado por
se repetirão) gerado por 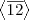 .
.

Cleyson007 escreveu:Renato, se não for incomodo demonstre por favor que H ? K é um subgrupo.
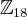 com a operação de soma, então:
com a operação de soma, então: e
e  por definição, logo
por definição, logo 
 . Como H é subgrupo de
. Como H é subgrupo de 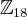 e
e 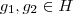 então
então 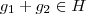 . Analogamente para K, então
. Analogamente para K, então 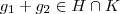 .
.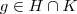 , como H é subgrupo então existe
, como H é subgrupo então existe  . Analogamente para K, então
. Analogamente para K, então 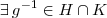
 é subgrupo de
é subgrupo de 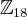 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes

 .
.
 :
: