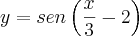
Me passaram da seguinte forma:
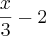
--------------------------------------------------------------------




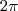
================================================
x
------------------------------------------------------------------
6=343º
3
 -43/2=613º
-43/2=613º 3
 +6=883º
+6=883º9
 +6/2=1153º
+6/2=1153º6
 +6+1425
+6+1425 ===============================================
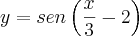
-------------------------------------------------------------------
Sen 0 = 0
Sen
 = 1
= 1Sen
 += 0
+= 0Sen
 =-1
=-1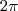 =0
=0================================================
Porém eu fiz diferente, acredito que esteja errado. Ajuda?




 , avisa que eu resolvo.
, avisa que eu resolvo.

