 por Danilo » Sex Ago 16, 2013 16:51
por Danilo » Sex Ago 16, 2013 16:51
Eu quero fatorar
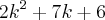
e não sei como. Eu sei um polinômio de raizes z1 e z2 de equação
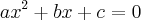
eu posso fatorar
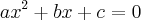
= a (x-z1) (x-z2). Mas eu não consigo aplicar isso no polinômio
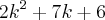
. Por que não consigo?
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Sobreira » Sex Ago 16, 2013 17:47
por Sobreira » Sex Ago 16, 2013 17:47
Você pode encontrar as soluções desta equação através de Bháskara:
Encontrará:

e

A partir disto você pode colocar da forma como você mesmo comentou:
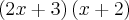
Para você testar se está certo, você pode multiplicar os termos internos e externos e somá-los, este será o segundo termo do trinômio descrito.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por Russman » Sex Ago 16, 2013 18:14
por Russman » Sex Ago 16, 2013 18:14
Pq não consegue? As raízes são
![-frac{3}{2}[tex] e -frac{3}{2}[tex] e](/latexrender/pictures/86f61404118907c8eb2447bd896603e5.png)
-2[/tex] de modo que a fatoração será

Veja que
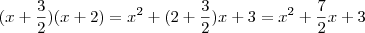
e que multiplicado por 2 resulta em

que é a forma original.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Danilo » Sex Ago 16, 2013 18:16
por Danilo » Sex Ago 16, 2013 18:16
Valeu. To resolvendo um exercício de indução e queria chegar ''lá'' mais rápido. Obrigado.
-
Danilo
- Colaborador Voluntário

-
- Mensagens: 224
- Registrado em: Qui Mar 15, 2012 23:36
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatoração de polinomios
por theSinister » Ter Mai 10, 2011 20:23
- 1 Respostas
- 1761 Exibições
- Última mensagem por MarceloFantini

Ter Mai 10, 2011 21:33
Álgebra Elementar
-
- [Polinomios] Fatoração
por carvalhothg » Ter Set 20, 2011 18:08
- 3 Respostas
- 1952 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 19:19
Polinômios
-
- [fatoração de polinômios]
por jvabatista » Qua Abr 18, 2012 01:42
- 7 Respostas
- 4201 Exibições
- Última mensagem por DanielFerreira

Dom Abr 29, 2012 00:42
Polinômios
-
- Fatoração de polinômios
por Danilo » Sáb Jul 28, 2012 12:45
- 2 Respostas
- 1688 Exibições
- Última mensagem por Danilo

Sáb Jul 28, 2012 14:03
Polinômios
-
- Fatoração de Polinômios
por matheus_frs1 » Sex Mar 18, 2016 22:49
- 1 Respostas
- 1975 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 16, 2016 23:08
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
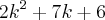 e não sei como. Eu sei um polinômio de raizes z1 e z2 de equação
e não sei como. Eu sei um polinômio de raizes z1 e z2 de equação 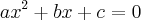 eu posso fatorar
eu posso fatorar 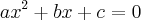 = a (x-z1) (x-z2). Mas eu não consigo aplicar isso no polinômio
= a (x-z1) (x-z2). Mas eu não consigo aplicar isso no polinômio 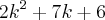 . Por que não consigo?
. Por que não consigo?
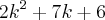 e não sei como. Eu sei um polinômio de raizes z1 e z2 de equação
e não sei como. Eu sei um polinômio de raizes z1 e z2 de equação 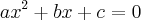 eu posso fatorar
eu posso fatorar 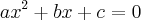 = a (x-z1) (x-z2). Mas eu não consigo aplicar isso no polinômio
= a (x-z1) (x-z2). Mas eu não consigo aplicar isso no polinômio 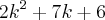 . Por que não consigo?
. Por que não consigo?
 e
e 
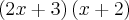
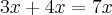

![-frac{3}{2}[tex] e -frac{3}{2}[tex] e](/latexrender/pictures/86f61404118907c8eb2447bd896603e5.png) -2[/tex] de modo que a fatoração será
-2[/tex] de modo que a fatoração será
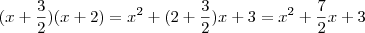 e que multiplicado por 2 resulta em
e que multiplicado por 2 resulta em




 , avisa que eu resolvo.
, avisa que eu resolvo.

