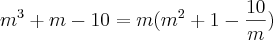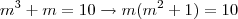por Pessoa Estranha » Ter Ago 13, 2013 19:51
por Pessoa Estranha » Ter Ago 13, 2013 19:51
Olá. Gostaria que alguém resolvesse este exercício, pois tentei de diversas maneiras e várias vezes, mas não consegui resolvê-lo. Obrigada.
Questão: Determine m e n tais que (u,v) (sequência dos vetores u e v) seja linearmente dependente (LD), sendo u = (1, m, n+1) e v = (m, n, 10).
Tentei usar a Proposição que envolve determinantes, combinação linear, proporção, equação tal que a solução não seja a trivial, mas nada resolveu.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Ter Ago 13, 2013 22:30
por Russman » Ter Ago 13, 2013 22:30
O vetor u tem de ser LD de v, é isso?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Qua Ago 14, 2013 17:38
por Pessoa Estranha » Qua Ago 14, 2013 17:38
Na verdade é que a sequência de vetores u e v seja LD, ou seja, o conjunto formado por estes dois vetores é LD. Por exemplo: se uma sequência de vetores é LD, então estes vetores são paralelos, ou podemos dizer que há uma combinação linear entre eles, etc. Agora, se uma sequência de vetores é LI, então estes vetores não são paralelos, ou então podemos pensar que não há uma combinação entres eles, etc.
Acho que, de certa forma, o que você disse está correto, mas o que eu entendo por (u, v) LD é o que escrevi acima.
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qua Ago 14, 2013 20:46
por Russman » Qua Ago 14, 2013 20:46
Sim, eu entendo o que significa um conjunto LI e LD. Só achei, de imediato, estranho o conjunto ter só dois elementos. Mas, sendo assim, deve existir um n° real

tal que
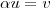
Isto é


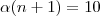
.
Da primeira linha podemos reescrever as duas outras como
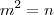
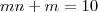
de onde, substituindo a 1° na segunda,
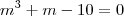
.
A única solução real desta equação é
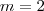
, de modo que

e

. Sendo assim,
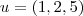
e
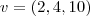
.
Bem verdade que

.
Certo?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Qua Ago 14, 2013 21:53
por Pessoa Estranha » Qua Ago 14, 2013 21:53
Olá. A resposta é essa mesmo! Muito bom! Mas, como você conseguiu resolver a equação do terceiro grau?! Nossa, estou pasma! Tentei diversas vezes e nada funcionou. Muito obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qua Ago 14, 2013 22:25
por Russman » Qua Ago 14, 2013 22:25
Bom, analisando a equação eu percebi que
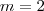
era solução. Aí, reduzi a equação para uma de 2° grau e está nao tem soluções reais. Logo, a única solução real é
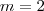
mesmo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Qui Ago 15, 2013 16:03
por Pessoa Estranha » Qui Ago 15, 2013 16:03
Para reduzir a equação ao segundo grau, você colocou o m em evidência?
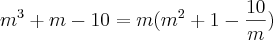
ou, então
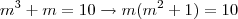
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por Russman » Qui Ago 15, 2013 16:10
por Russman » Qui Ago 15, 2013 16:10
Não. A sua fatoração não lhe ajudará a resolver. Como m=2 é soluçào, então a equação ê divisível por (m-2). Tente fazer isso.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Pessoa Estranha » Qui Ago 15, 2013 16:14
por Pessoa Estranha » Qui Ago 15, 2013 16:14
Ok. Valeu!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria Analítica - Dependência Linear
por -civil- » Sex Abr 22, 2011 13:29
- 1 Respostas
- 1498 Exibições
- Última mensagem por NMiguel

Sex Abr 22, 2011 14:16
Geometria Analítica
-
- [Geometria Analítica] Dependência Linear.
por Pessoa Estranha » Sex Ago 02, 2013 16:14
- 4 Respostas
- 2742 Exibições
- Última mensagem por Pessoa Estranha

Sáb Ago 03, 2013 11:17
Geometria Analítica
-
- [Geometria Analítica] Dependência e independência linear
 por Aliocha Karamazov » Qua Out 12, 2011 12:43
por Aliocha Karamazov » Qua Out 12, 2011 12:43
- 2 Respostas
- 2325 Exibições
- Última mensagem por Aliocha Karamazov

Qua Out 26, 2011 21:57
Geometria Analítica
-
- Algebra linear e geometria analítica
por clari_27 » Sáb Mai 12, 2012 17:32
- 1 Respostas
- 1905 Exibições
- Última mensagem por LuizAquino

Seg Mai 14, 2012 10:56
Geometria Analítica
-
- Geometria Analitica e Algebra linear
por Danizinhalacerda13 » Qui Mai 01, 2014 19:15
- 1 Respostas
- 2898 Exibições
- Última mensagem por Danizinhalacerda13

Qui Mai 01, 2014 19:25
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 tal que
tal que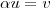


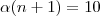 .
.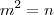
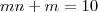
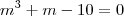 .
.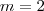 , de modo que
, de modo que  e
e  . Sendo assim,
. Sendo assim,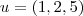
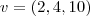 .
. .
.