Tentei resolver este problema de todas as formas, mais não consigo chegar ao resultado, sei que o resultado é 295, mais gostaria de saber como chegar nele, por favor me ajudem, pois estou estudando para outro concurso.
segue o problema...
Suponha que, na venda de x unidades de certo artigo, o lucro obtido seja calculado pela fórmula L(x)=6x-C(x), em que C(x), é o custo da produção de tal artigo. Considerando que C(x), em reais, é dado pela expressão C(x)=150+2x/5, então, para que seja obtido um lucro, superior a R$1.500,00 a menor quatidade de artigos que devem ser vendidos é igual a
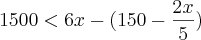
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png "\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}")
![\sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png "\sqrt[]{2}")
e elevar ao quadrado os dois lados)