Regras do fórum
A classificação destes desafios em fáceis, médios e difíceis, é apenas ilustrativa.
Eventualmente, o que pode ser difícil para a maioria, pode ser fácil para você e vice-versa.
 por ericomoura » Ter Nov 17, 2009 12:03
por ericomoura » Ter Nov 17, 2009 12:03
Gente, achei um desafio que, na minha opinião é quase impossível. O desafio é o seguinte:
ObjetivoConseguir todos os números do relógio
Regras-Você OBRIGATORIAMENTE tem que usar 3 noves
-Você não pode usar nenhum outro número que não seja o número nove (nem raiz quadrada, que é raiz de 2)
Obs.:-O número 99 conta como dois noves
-Potência 9 e raiz nona tambem contam como nove, ou seja

conta como dois noves e
![\sqrt[9]{9} \sqrt[9]{9}](/latexrender/pictures/437abc99dfab74ed59bfaed7b8a07785.png)
também conta como dois noves
-Você pode usar QUALQUER conta matemática para resolver isso.
Bem gente, esse é o desafio. Até agora eu só consegui o
1=

2=(9+9)/9
3=????
4=????
5=????
6=????
7=????
8=9-9/9
9=9+9-9
10=(9/9)+9
11=99/9
12=????
Por favor me ajudem

Obrigado
-
ericomoura
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Ter Nov 17, 2009 11:42
- Formação Escolar: ENSINO FUNDAMENTAL II
- Área/Curso: Estudante
- Andamento: cursando
 por Molina » Ter Nov 17, 2009 15:05
por Molina » Ter Nov 17, 2009 15:05
Boa tarde, amigo!
Sem usar raiz acho que é realmente impossível.
Mas não custa tentar

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Neperiano » Qui Set 23, 2010 17:47
por Neperiano » Qui Set 23, 2010 17:47
Ola
Só usando 3 casas é impossivel, mas vamos tentar
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por Balanar » Qua Out 13, 2010 14:34
por Balanar » Qua Out 13, 2010 14:34
Editado pela última vez por
Balanar em Qua Out 13, 2010 17:52, em um total de 1 vez.
-
Balanar
- Usuário Parceiro

-
- Mensagens: 72
- Registrado em: Qua Dez 03, 2008 07:18
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Neperiano » Qua Out 13, 2010 16:53
por Neperiano » Qua Out 13, 2010 16:53
Ola
Não pode aplicar 9 na 0 esse que é o problema
Atenciosamente
Sómente os mortos conhecem o fim da guerra
"Platão"
-

Neperiano
- Colaborador Voluntário

-
- Mensagens: 960
- Registrado em: Seg Jun 16, 2008 17:09
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
 por victoreis1 » Qui Out 21, 2010 20:07
por victoreis1 » Qui Out 21, 2010 20:07
já que vc disse QUALQUER operação..

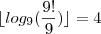


![\lfloor{9 - \sqrt[9]{9}}\rfloor = 7 \lfloor{9 - \sqrt[9]{9}}\rfloor = 7](/latexrender/pictures/4e06689635e13bd1a6273778967d05cc.png)
essa última foi especialmente perfeita:
![\lceil{log_\sqrt[9]{9} \lceil{log_\sqrt[9]{9}](/latexrender/pictures/336a1ca1e8d27cd8fcc1f31aef1eda53.png)

( e também super difícil de escrever no latex)
na matemática, nada é impossível! haha
ObservaçãoVide a página
"Parte inteira" para detalhes dos operadores

(chão) e

(teto).
-
victoreis1
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qua Out 20, 2010 14:49
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qua Fev 09, 2011 18:47
por Molina » Qua Fev 09, 2011 18:47
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Qua Fev 09, 2011 22:01
por Dan » Qua Fev 09, 2011 22:01
Molina e Balanar, vocês sabem que pelas regras não pode usar raíz quadrada.
É um detalhe que passa invisível, né?
Ou seja, voltamos todos à estaca zero.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Molina » Qua Fev 09, 2011 23:14
por Molina » Qua Fev 09, 2011 23:14
Dan escreveu:Molina e Balanar, vocês sabem que pelas regras não pode usar raíz quadrada.
É um detalhe que passa invisível, né?
Ou seja, voltamos todos à estaca zero.
Sim, Dan.
Pela regra nao se pode usar.
Mas nao vejo outro modo sem usar raiz..
Acho que foi ate comentado isso anteriormente.

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Dan » Qui Fev 10, 2011 12:21
por Dan » Qui Fev 10, 2011 12:21
Tudo bem, Molina.
Eu só considero mais interessante e desafiador não usar raíz quadrada.
-

Dan
- Colaborador Voluntário

-
- Mensagens: 101
- Registrado em: Seg Set 14, 2009 09:44
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Desafios Difíceis
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:46
- 1 Respostas
- 2658 Exibições
- Última mensagem por Felipe Schucman

Qui Jul 30, 2009 18:09
Trigonometria
-
- Relógio
por DanielFerreira » Qui Jul 30, 2009 17:50
- 2 Respostas
- 4073 Exibições
- Última mensagem por Elcioschin

Sáb Ago 01, 2009 13:02
Desafios Médios
-
- Ângulo Relógio
por estudandoMat » Sex Abr 02, 2010 12:38
- 2 Respostas
- 6977 Exibições
- Última mensagem por estudandoMat

Sex Abr 02, 2010 14:49
Trigonometria
-
- Ponteiro de relógio
por Rafael16 » Seg Mai 27, 2013 22:07
- 1 Respostas
- 2515 Exibições
- Última mensagem por Molina

Ter Mai 28, 2013 19:59
Trigonometria
-
- Ângulos no Relógio
por miguel135 » Sex Mar 28, 2014 17:02
- 11 Respostas
- 10041 Exibições
- Última mensagem por Isis

Qua Abr 30, 2014 12:02
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 conta como dois noves e
conta como dois noves e ![\sqrt[9]{9} \sqrt[9]{9}](/latexrender/pictures/437abc99dfab74ed59bfaed7b8a07785.png) também conta como dois noves
também conta como dois noves





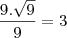


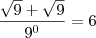

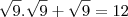



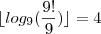


![\lfloor{9 - \sqrt[9]{9}}\rfloor = 7 \lfloor{9 - \sqrt[9]{9}}\rfloor = 7](/latexrender/pictures/4e06689635e13bd1a6273778967d05cc.png)
![\lceil{log_\sqrt[9]{9} \lceil{log_\sqrt[9]{9}](/latexrender/pictures/336a1ca1e8d27cd8fcc1f31aef1eda53.png)
 ( e também super difícil de escrever no latex)
( e também super difícil de escrever no latex) (chão) e
(chão) e  (teto).
(teto).
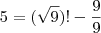


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.