quadrado com triângulos construídos em seu interior

por **geobson** » Sáb Ago 03, 2013 23:09

há mais de um mês tento conseguir uma solução para o problema abaixo . por favor , se alguém puder me ajudar com a solução ou pelo menos com uma dica , ficarei muito agradecido.

seja E um ponto interior de um quadrado ABCD , de modo que AE=c, BE=a e CE=a + b, onde a² + b² = c² . A medida do ângulo BÊC é igual a :

a)30º
b)45º
c)60º
d)90º
e)120º
f)135º

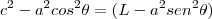
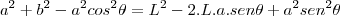
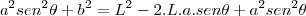
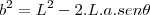
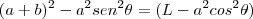
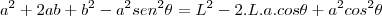
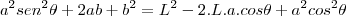
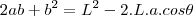
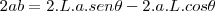
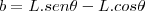
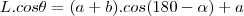
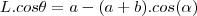
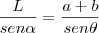
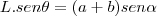
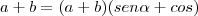
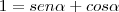
por **young_jedi** » Seg Ago 05, 2013 19:49

amigo, entendi que o desenho da questão fica da seguinte maneira

: quad.png (3.21 KiB) Exibido 754 vezes

considerando que o lado do quadrado vale L nos podemos tirar as seguintes relações analisando o trianguloa AEB

$c^2-a^2cos^2\theta=(L-a^2sen^2\theta)$

$a^2+b^2-a^2cos^2\theta=L^2-2.L.a.sen\theta+a^2sen^2\theta$

$a^2sen^2\theta+b^2=L^2-2.L.a.sen\theta+a^2sen^2\theta$

$b^2=L^2-2.L.a.sen\theta$

analisando o triangulo BEC tiramos

$(a+b)^2-a^2sen^2\theta=(L-a^2cos^2\theta)$

$a^2+2ab+b^2-a^2sen^2\theta=L^2-2.L.a.cos\theta+a^2cos^2\theta$

$a^2sen^2\theta+2ab+b^2=L^2-2.L.a.cos\theta+a^2cos^2\theta$

$2ab+b^2=L^2-2.L.a.cos\theta$

subtraindo a primeira equação encontrada da segunda temos

$2ab=2.L.a.sen\theta-2.a.L.cos\theta$

$b=L.sen\theta-L.cos\theta$

fazendo uma segunda analise da figura temos

: quad2.png (4.16 KiB) Exibido 754 vezes

dai tiramos a seguinte relação

$L.cos\theta=(a+b).cos(180-\alpha)+a$

$L.cos\theta=a-(a+b).cos(\alpha)$

e pela lei dos senos tiramos que

$\frac{L}{sen\alpha}=\frac{a+b}{sen\theta}$

$L.sen\theta=(a+b)sen\alpha$

substituindo essa relação na equação $b=L.sen\theta-L.cos\theta$ temos

$b=(a+b).sen\alpha-a+(a+b).cos\alpha$

$a+b=(a+b)(sen\alpha+cos\lapha)$

$1=sen\alpha+cos\alpha$

resolvendo esta equação chegamos em $\alpha=90^o$

quadrado com triângulos construídos em seu interior

quadrado com triângulos construídos em seu interior

quadrado com triângulos construídos em seu interior

Re: quadrado com triângulos construídos em seu interior

Quem está online