(UECE) Seja (a1, a2, a3, a4, a5, a6, a7, a8) uma progressão aritmética. Se a2+a5=8 e a8=7, então a3+a7 é igual a:
a) 8
b) 28/3
c) 10
d) 32/3
Não consigo desenvolver um raciocínio para resolver este problema.




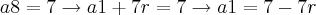
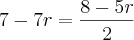

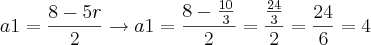
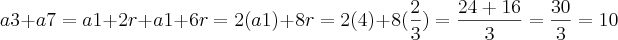

Pessoa Estranha escreveu:Olá. Segue o meu raciocínio. Espero que entenda.
Como trata-se de uma progressão aritmética, sabemos que estamos trabalhando em função do primeiro termo (a1) e da razão (podemos chamar de "r"). Observe que o segundo termo, por exemplo, nada mais é do que o primeiro termo somado com a razão. Agora, note que podemos pensar assim também: o terceiro termo, por exemplo, corresponde à soma do primeiro termo com duas vezes a razão (a3 = a1 + 2r) ou à soma do segundo termo com a razão (a3 = a2 + r). E este raciocínio segue sucessivamente. Bem, o enunciado do problema diz que trata-se de uma progressão aritmética e nos traz duas informações importantes: a2 + a5 = 8 e a8 = 7. Assim, note que podemos fazer o seguinte:
Daí, podemos igualar as duas expressões encontradas. Veja:
Então:
Daí, como temos o valor da razão, podemos encontrar o valor do primeiro termo:
Assim:
Alternativa C.
Tem o gabarito? Se tiver mande uma resposta dizendo se está correto.
Espero ter ajudado.

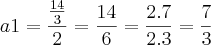
 .
.

Pessoa Estranha escreveu:Você tem razão. Peço desculpas pelo meu erro grave.
O correto é:.
Desculpe.


Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.