Nós aqui do fórum achamos mais producente que você ao expor suas dúvidas exponha junto com elas a sua tentativa de resolução para que possamos te ajudar a resolver a questão ao invés de resolvê-la por você. Mas como estou com tempo agora eu vou deixar a solução aqui. Mas procure, futuramente, não repetir esse comportamento para o próprio bem do seu aprendizado.
25)
O exercício pede que você calcule a taxa de variação (TDV) da área do triângulo com relação a variação do catetos. Assim, a primeira coisa a ser feita é expressar a área em função destes, certo?
Como o triângulo é retângulo a sua área é dada pela metade do produto dos catetos. Sejam
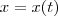
e

os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por
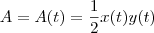
de modo que
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)]](/latexrender/pictures/1a34075169e113ffc583d801742964d0.png)
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ]](/latexrender/pictures/cdeb48e51d261a2ada33e8fa596743a2.png)
e , portanto,
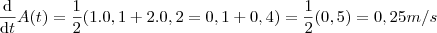
.
26)
Para resolver esta basta fazer exatamente o que fiz na questão anterior. Expresse o volume do cone em função da altura e do raio de base, derive e voilà.



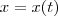 e
e  os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por
os catetos do triângulo que são função do tempo, pois seus comprimentos variam linearmente com o mesmo. Assim, a área , que também é função do tempo será dada por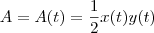
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} \frac{\mathrm{d} }{\mathrm{d} t}[x(t)y(t)]](/latexrender/pictures/1a34075169e113ffc583d801742964d0.png)
![\frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ] \frac{\mathrm{d} }{\mathrm{d} t} A(t) = \frac{1}{2} [x \frac{\mathrm{d} }{\mathrm{d} t}y + y \frac{\mathrm{d} }{\mathrm{d} t}x ]](/latexrender/pictures/cdeb48e51d261a2ada33e8fa596743a2.png)
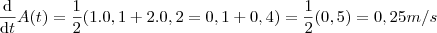 .
.


