 por armando » Seg Jul 29, 2013 23:53
por armando » Seg Jul 29, 2013 23:53
Boa noite a todos.
Considerem a seguinte integral:
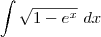
Qual o processo de resolução a usar ? Por partes ? Por substituição ... ?
Grato pela atenção.
armando
-
armando
- Usuário Dedicado

-
- Mensagens: 26
- Registrado em: Seg Abr 01, 2013 16:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Russman » Ter Jul 30, 2013 00:30
por Russman » Ter Jul 30, 2013 00:30
Substituição!
Faça

e depois
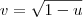
que eu acho que funciona.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por MateusL » Ter Jul 30, 2013 02:47
por MateusL » Ter Jul 30, 2013 02:47
Faça
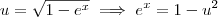
.
Teremos:
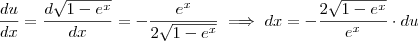
Assim:
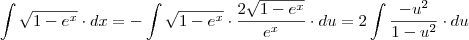
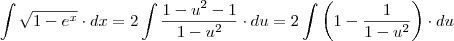
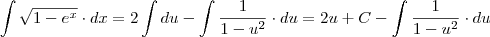
Só não consegui encontrar uma maneira de resolver
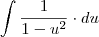
(sem ser utilizando o WolframAlpha).
Abraço
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Ter Jul 30, 2013 03:13
por Russman » Ter Jul 30, 2013 03:13
Basta tomar
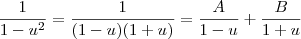
onde
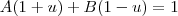
.
Logo,
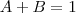
e
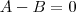
de modo que
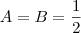
e, portanto,
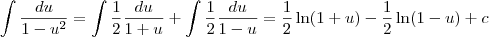
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Man Utd » Ter Jul 30, 2013 11:26
por Man Utd » Ter Jul 30, 2013 11:26
também poderia resolver de imediato assim:
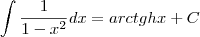
Editado pela última vez por
Man Utd em Ter Jul 30, 2013 19:29, em um total de 1 vez.
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Man Utd » Ter Jul 30, 2013 15:31
por Man Utd » Ter Jul 30, 2013 15:31
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Russman » Ter Jul 30, 2013 17:24
por Russman » Ter Jul 30, 2013 17:24
De imediato? Haha
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Man Utd » Ter Jul 30, 2013 19:31
por Man Utd » Ter Jul 30, 2013 19:31
é mais ligeiro que fazer por frações parciais né?
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Russman » Ter Jul 30, 2013 19:38
por Russman » Ter Jul 30, 2013 19:38
Mas como voce demonstra o resultado se não por fraçoes parciais? A diferença daqueles logaritmos é, por definição, o arco tangente hiperbólico.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Man Utd » Ter Jul 30, 2013 19:58
por Man Utd » Ter Jul 30, 2013 19:58
eu não posso demosntrar assim?
pela definição da derivada função inversa:
f(x)=tgh x---------f¹(x)=arc tgh x
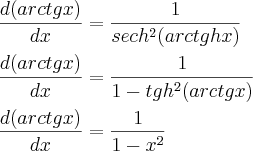
tem certeza que você ñ acha mais prático?
único ponto negativo que eu vejo é a memorização,mas a dedução é extremamente fácil.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por Russman » Ter Jul 30, 2013 20:06
por Russman » Ter Jul 30, 2013 20:06
Eu ainda acho mais simples usando as exponenciais. Mas tudo bem, diversos caminhos levam à Roma.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Man Utd » Ter Jul 30, 2013 20:09
por Man Utd » Ter Jul 30, 2013 20:09
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [INTEGRAL INDEFINIDA] Qual será aSubstituição?
por fabriel » Sex Out 05, 2012 02:47
- 4 Respostas
- 2749 Exibições
- Última mensagem por fabriel

Sex Out 05, 2012 17:22
Cálculo: Limites, Derivadas e Integrais
-
- Resolução de integral indefinida
por jearaujo01 » Seg Mar 07, 2016 15:46
- 0 Respostas
- 1875 Exibições
- Última mensagem por jearaujo01

Seg Mar 07, 2016 15:46
Cálculo: Limites, Derivadas e Integrais
-
- Integral - Resolução de integral indefinida.
por brunoisoppo » Qui Mar 03, 2016 15:26
- 0 Respostas
- 3445 Exibições
- Última mensagem por brunoisoppo

Qui Mar 03, 2016 15:26
Cálculo: Limites, Derivadas e Integrais
-
- duvida qual calculo usar
por smallville » Sex Fev 12, 2010 10:13
- 1 Respostas
- 1236 Exibições
- Última mensagem por Molina

Sex Fev 12, 2010 11:40
Trigonometria
-
- qual é a integral indefinida passo-a-passo de:
por Raphison » Seg Dez 01, 2014 10:53
- 2 Respostas
- 1609 Exibições
- Última mensagem por Raphison

Qua Dez 03, 2014 08:42
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
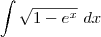

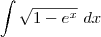

 e depois
e depois 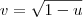 que eu acho que funciona.
que eu acho que funciona.
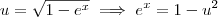 .
.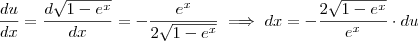
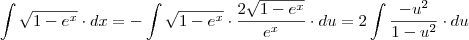
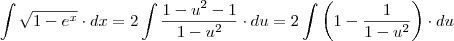
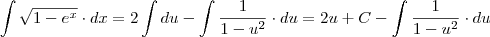
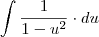 (sem ser utilizando o WolframAlpha).
(sem ser utilizando o WolframAlpha).
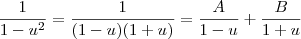
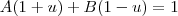 .
.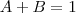 e
e 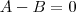 de modo que
de modo que 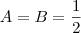 e, portanto,
e, portanto, 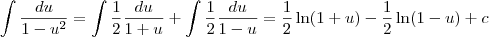

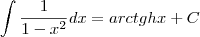












 , avisa que eu resolvo.
, avisa que eu resolvo.

