(PUC-RJ) João dá a Pedro tantos reais quanto Pedro
possui. Em seguida, Pedro dá a João tantos reais quanto
João possui. Se terminaram com R$180,00 cada um,
quantos reais cada um deles possuía inicialmente?
a) João possuía R$100,00 e Pedro R$80,00.
b) João possuía R$200,00 e Pedro R$225,00.
c) João possuía R$135,00 e Pedro R$280,00.
d) João possuía R$225,00 e Pedro R$135,00.
e) João possuía R$100,00 e Pedro R$135,00.
Resposta: D
é fácil deduzir a resposta, mas eu não conseguir montar um sistema para responder essa questão, assim poderei responder outras do mesmo tipo:
Eu tentei criar um sistema do primeiro grau igualando as variáveis, mas não conseguir entender e nem montar o sistema.
Agradeceria uma explicação para melhor compreensão de resolver o problema.


 onde
onde  é uma variável que indica a vez-troca de dinheiro. Portanto, de início, João tem
é uma variável que indica a vez-troca de dinheiro. Portanto, de início, João tem 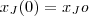 reais e Pedro
reais e Pedro  reais.
reais.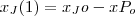 e
e  . Se, em seguida, Pedro dá a João tantos reais quanto João possui, então
. Se, em seguida, Pedro dá a João tantos reais quanto João possui, então 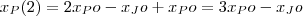 e
e  .
.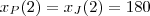 e o sistema de equações apresenta-se como
e o sistema de equações apresenta-se como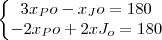
 e
e  .
.
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.