 por Pessoa Estranha » Ter Jul 23, 2013 12:54
por Pessoa Estranha » Ter Jul 23, 2013 12:54
Olá.... Por favor, me ajudem a calcular estes limites. Eles envolvem logaritmos na base

. Tentei resolvê-los, mas no primeiro, a minha resposta deu zero; no segundo, deu indeterminação; e no terceiro, não consegui chegar a uma resposta.
Obrigada.
d)
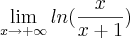
e)
![\lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]} \lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]}](/latexrender/pictures/136d53d608e1e5ac90152c502ea6f603.png)
g)
![\lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}} \lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}}](/latexrender/pictures/bb61cd5d6ef792fa89c97ed5a34e582f.png)
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Ter Jul 23, 2013 19:58
por young_jedi » Ter Jul 23, 2013 19:58
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Qua Jul 24, 2013 11:17
por Pessoa Estranha » Qua Jul 24, 2013 11:17
Ótimas as respostas! Valeu!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmos] Dúvida em um exercicio envolvendo logaritmos.
por LuizGustavo » Sex Jun 01, 2012 22:48
- 2 Respostas
- 5031 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- [Logaritmos] equação com logaritmos
por natanaelvoss » Sex Dez 07, 2012 20:25
- 2 Respostas
- 6661 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:40
Logaritmos
-
- logaritmos
por celisecorrea » Ter Set 30, 2008 17:17
- 2 Respostas
- 3352 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:38
Logaritmos
-
- LOGARITMOS
por DESESPERADA » Qua Dez 30, 2009 13:25
- 2 Respostas
- 3122 Exibições
- Última mensagem por jefferson0209

Ter Set 22, 2015 18:37
Matemática Financeira
-
- Logaritmos
por cristina » Qua Jun 02, 2010 10:07
- 1 Respostas
- 2416 Exibições
- Última mensagem por Cleyson007

Qua Jun 02, 2010 13:30
Logaritmos
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 . Tentei resolvê-los, mas no primeiro, a minha resposta deu zero; no segundo, deu indeterminação; e no terceiro, não consegui chegar a uma resposta.
. Tentei resolvê-los, mas no primeiro, a minha resposta deu zero; no segundo, deu indeterminação; e no terceiro, não consegui chegar a uma resposta.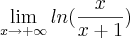
![\lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]} \lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]}](/latexrender/pictures/136d53d608e1e5ac90152c502ea6f603.png)
![\lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}} \lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}}](/latexrender/pictures/bb61cd5d6ef792fa89c97ed5a34e582f.png)

 . Tentei resolvê-los, mas no primeiro, a minha resposta deu zero; no segundo, deu indeterminação; e no terceiro, não consegui chegar a uma resposta.
. Tentei resolvê-los, mas no primeiro, a minha resposta deu zero; no segundo, deu indeterminação; e no terceiro, não consegui chegar a uma resposta.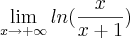
![\lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]} \lim_{x\rightarrow+\infty}{[ln(2x+1)-ln(x+3)]}](/latexrender/pictures/136d53d608e1e5ac90152c502ea6f603.png)
![\lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}} \lim_{x\rightarrow+\infty}{{[[x.ln(2)]-ln({3}^{x}+1)]}}](/latexrender/pictures/bb61cd5d6ef792fa89c97ed5a34e582f.png)


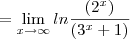
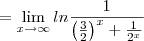
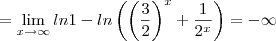

![\lim_{x\to +\infty}[\ln(2x+1)-\ln(x+3)]=\lim_{x\to +\infty}\ln\left(\dfrac{2x+1}{x+3}\right) \lim_{x\to +\infty}[\ln(2x+1)-\ln(x+3)]=\lim_{x\to +\infty}\ln\left(\dfrac{2x+1}{x+3}\right)](/latexrender/pictures/89625eef3bb0221adf8dfb686990367d.png)






 , avisa que eu resolvo.
, avisa que eu resolvo.

