Dada a função :
![f(x)=\sqrt[3]{\frac{3}{x^2}} f(x)=\sqrt[3]{\frac{3}{x^2}}](/latexrender/pictures/3aba0e9abab4f0ba5ddc428e9fa88019.png)
Tenho dúvidas quanto à solução dada no livro de onde retirei a questão. Que é como se segue:
![f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5} f^,(x)=-\frac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}](/latexrender/pictures/10452201c2b2f1c7eada127ab33aa66d.png)
Tanto quanto sei a fórmula para a derivada de uma raiz é :

ou, esta outra:
![y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^, y^,=\frac{1}{k\sqrt[k]{u^{k-1}}}\cdot u^,](/latexrender/pictures/9dc847524b7f60ef3b880bb257f3e76b.png)
A derivada do radicando,

 aplicando a fórmula de resolução do quociente dá
aplicando a fórmula de resolução do quociente dá 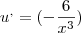 . Aplicando no lugar correto da/s fórmula/s, e desenvolvendo qualquer uma delas na integra deveríamos chegar á solução dada. Facto que aliás não consegui.
. Aplicando no lugar correto da/s fórmula/s, e desenvolvendo qualquer uma delas na integra deveríamos chegar á solução dada. Facto que aliás não consegui.A minha dúvida é a seguinte:__ Será que a solução está errada ? Ou me estão faltando alguns artifícios matemáticos para conseguir chegar a ela ?
Gostava que alguém resolvesse a questão na integra,até à simplificação máxima para verificação, e assim tirar minha dúvida.
Grato pela atenção
armando



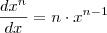
![f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3} f(x)=\sqrt[3]{3}\cdot x^\frac{-2}{3}](/latexrender/pictures/77ede464f588caa699d9e91317e3f498.png)

![f(x)=\sqrt[5]{\frac{3}{x^2}} f(x)=\sqrt[5]{\frac{3}{x^2}}](/latexrender/pictures/e288236abb7391f8f3db51c4d1a3f2d4.png) ?
?![f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}} f(x)=\sqrt[5]{3}\cdot x^{-\frac{2}{5}}](/latexrender/pictures/7419eae39890ed57c091e8b620b854c9.png)
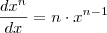 :
:![\dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}} \dfrac{df(x)}{dx}=\dfrac{d(\sqrt[5]{3}\cdot x^{-\frac{2}{5}})}{dx}=\sqrt[5]{3}\cdot \dfrac{d x^{-\frac{2}{5}}}{dx}=\sqrt[5]{3}\cdot \dfrac{-2}{5}\cdot x^{-\frac{2}{5}-1}=-\dfrac{2\sqrt[5]{3}}{5}\cdot x^{-\frac{7}{5}}](/latexrender/pictures/a409d25c37b6ad04d15e52b0b213b833.png)

 .
.
 :
: