 por Jhonata » Qua Jul 17, 2013 18:46
por Jhonata » Qua Jul 17, 2013 18:46
Olá pessoal!
Bem, eu estou com dificuldades de entender "mudança de base", um tópico da álgebra linear aparentemente muito importante.
Me deparei com o seguinte problema:
Sejam

e

duas bases do
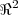
. Determine a matriz de mudança de base

para a base

.
Minha resolução:
Escrevi os vetores da base

como CL da base canônica dada:
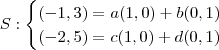
O sistema se resolve por si só, obtemos então: a = -1, b = 3, c = -2, d = 5.
A matriz da mudança de base será:
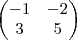
Mas o gabarito diz que a matriz da mudança de base é:
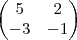
Alguém pode apontar onde estou errando?
Desde já, agradecido.
Att.
" A Matemática é a honra do espírito humano - Leibniz "
-

Jhonata
- Usuário Parceiro

-
- Mensagens: 66
- Registrado em: Sáb Mai 26, 2012 17:42
- Localização: Rio de Janeiro
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenheria Mecânica - UFRJ
- Andamento: cursando
 por fabriel » Ter Nov 26, 2013 01:45
por fabriel » Ter Nov 26, 2013 01:45
Vc fez o contrário, vc determinou a matriz de mudança de base \beta para a base \alpha.

Matemática, de modo algum, são fórmulas, assim como a música não são notas. (Y Jurquim)
-

fabriel
- Usuário Parceiro

-
- Mensagens: 88
- Registrado em: Ter Mai 22, 2012 16:04
- Localização: Chapadão do Sul-MS
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Mudança de Base] Matriz de mudança de base ? para ?.
por fabriel » Ter Nov 26, 2013 15:38
- 0 Respostas
- 2101 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:38
Álgebra Linear
-
- Matriz mudança de base
por krllm » Seg Jul 07, 2014 22:50
- 0 Respostas
- 1990 Exibições
- Última mensagem por krllm

Seg Jul 07, 2014 22:50
Geometria Analítica
-
- [Inversa da matriz de mudança de base] demosntração
por fabriel » Ter Nov 26, 2013 15:44
- 0 Respostas
- 1278 Exibições
- Última mensagem por fabriel

Ter Nov 26, 2013 15:44
Álgebra Linear
-
- Mudança de Base
por Bruhh » Sáb Nov 20, 2010 17:30
- 0 Respostas
- 1362 Exibições
- Última mensagem por Bruhh

Sáb Nov 20, 2010 17:30
Geometria Analítica
-
- [Mudança de Base]
por ewald » Sex Abr 13, 2012 00:20
- 0 Respostas
- 1411 Exibições
- Última mensagem por ewald

Sex Abr 13, 2012 00:20
Introdução à Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  duas bases do
duas bases do 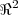 . Determine a matriz de mudança de base
. Determine a matriz de mudança de base  para a base
para a base  .
. como CL da base canônica dada:
como CL da base canônica dada: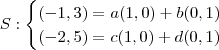
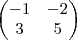
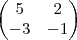



 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.