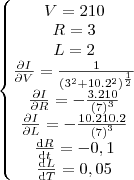por jpreis » Seg Jul 15, 2013 23:10
por jpreis » Seg Jul 15, 2013 23:10
Fala Galera, blz? Peço a gentileza de me ajudar no seguinte problema:
"Num determinado circuito elétrico, a corrente 'I' é dada, em função da voltagem 'V', da resistência 'R' e da indutância 'L' por
![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png)
. No instante em que 'V' é 210 volts, R é igual a 3 ohms e está decaindo a uma taxa de 0,1 ohms por segundo, enquanto que 'L' é igual a 2 henrys e está crescendo a uma razão de 0,05 henrys por segundo. Qual deve ser a variação de 'V', neste instante, para que a corrente permaneça constante?". Resposta = 3 volts por segundo.
COMO TENTEI RESOLVER: primeiro achei o valor de I através da substituição dos valores fornecidos pelo enunciado na equação
![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png)
, ficando desta forma:
![I = \frac{210}{\sqrt[2]{49}} = 30 I = \frac{210}{\sqrt[2]{49}} = 30](/latexrender/pictures/6fcf1c943af983c604e6cc3e103f0bd9.png)
. Após encontrar o valor de I, este foi igualado às derivadas de I em função das variáveis

e multipliquei cada derivada parcial por sua respectiva taxa de variação
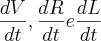
; lembrando que o valor que quero encontrar é
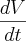
; assim ficou:

.
Resolvendo as derivadas, encontrei:
![\frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} \frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/5188559259bcaf6892cdd4568d69f646.png)
;
![\frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}} \frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}}](/latexrender/pictures/e597083528a8fa235ef71e3aed37b69f.png)
; e
![\frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}} \frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}}](/latexrender/pictures/336bcda187ceec6ab911e2912aaecf7d.png)
.
Fazendo desta forma encontrei um valor na ordem de 200, ou seja, muito distante da resposta correta (3 volts/s). Refiz diversas vezes e não saiu deste resultado.
Desde já agradeço a ajuda. Forte abraço!
jpreis
-
jpreis
- Novo Usuário

-
- Mensagens: 3
- Registrado em: Sáb Jul 13, 2013 14:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia
- Andamento: cursando
 por Russman » Ter Jul 16, 2013 00:36
por Russman » Ter Jul 16, 2013 00:36
O seu problema é inteiramente de Cálculo Diferencial. Voce tem uma função

que depende de 3 variáveis

,
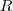
e

as quais dependem do tempo

. Assim, a derivada total de

será
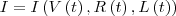
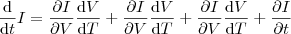
.
Dada a função, temos que
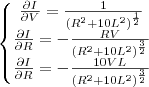
Se queremos calcular a variação de V, isto é,

no instante indicado, para que a corrente se mantenha constante, isto é,
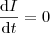
, então basta substituir na relação da derivada e teremos um resultado. Veja que no instante indicado temos
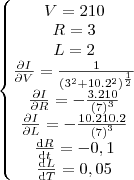
Agora substitua os valores, isole a derivada temporal de V e terá a solução.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Derivadas parciais
por john » Ter Fev 15, 2011 15:37
- 7 Respostas
- 6827 Exibições
- Última mensagem por john

Sáb Fev 19, 2011 16:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas parciais
por baianinha » Ter Jul 05, 2011 00:50
- 1 Respostas
- 2669 Exibições
- Última mensagem por MarceloFantini

Ter Jul 05, 2011 03:53
Cálculo: Limites, Derivadas e Integrais
-
- DERIVADAS PARCIAIS
por allyourwishes » Seg Jul 13, 2015 11:24
- 0 Respostas
- 2427 Exibições
- Última mensagem por allyourwishes

Seg Jul 13, 2015 11:24
Cálculo: Limites, Derivadas e Integrais
-
- Derivadas parciais
por caarolsnp » Sex Out 13, 2017 11:40
- 0 Respostas
- 4330 Exibições
- Última mensagem por caarolsnp

Sex Out 13, 2017 11:40
Cálculo: Limites, Derivadas e Integrais
-
- [otimização] DERIVADAS PARCIAIS
por montanha » Seg Ago 04, 2008 10:18
- 5 Respostas
- 13091 Exibições
- Última mensagem por admin

Sex Ago 08, 2008 15:14
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 7 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png) . No instante em que 'V' é 210 volts, R é igual a 3 ohms e está decaindo a uma taxa de 0,1 ohms por segundo, enquanto que 'L' é igual a 2 henrys e está crescendo a uma razão de 0,05 henrys por segundo. Qual deve ser a variação de 'V', neste instante, para que a corrente permaneça constante?". Resposta = 3 volts por segundo.
. No instante em que 'V' é 210 volts, R é igual a 3 ohms e está decaindo a uma taxa de 0,1 ohms por segundo, enquanto que 'L' é igual a 2 henrys e está crescendo a uma razão de 0,05 henrys por segundo. Qual deve ser a variação de 'V', neste instante, para que a corrente permaneça constante?". Resposta = 3 volts por segundo.![I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} I = \frac{V}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/e5cbbd819763792edfd0eaf70d035b72.png) , ficando desta forma:
, ficando desta forma: ![I = \frac{210}{\sqrt[2]{49}} = 30 I = \frac{210}{\sqrt[2]{49}} = 30](/latexrender/pictures/6fcf1c943af983c604e6cc3e103f0bd9.png) . Após encontrar o valor de I, este foi igualado às derivadas de I em função das variáveis
. Após encontrar o valor de I, este foi igualado às derivadas de I em função das variáveis  e multipliquei cada derivada parcial por sua respectiva taxa de variação
e multipliquei cada derivada parcial por sua respectiva taxa de variação 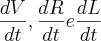 ; lembrando que o valor que quero encontrar é
; lembrando que o valor que quero encontrar é 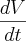 ; assim ficou:
; assim ficou:  .
. ![\frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}} \frac{\partial I}{\partial V} = \frac{1}{\sqrt[2]{{R}^{2}+10.{L}^{2}}}](/latexrender/pictures/5188559259bcaf6892cdd4568d69f646.png) ;
; ![\frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}} \frac{\partial I}{\partial R} = \frac{V}{L.\sqrt[2]{10}}.-\frac{1}{{R}^{2}}](/latexrender/pictures/e597083528a8fa235ef71e3aed37b69f.png) ; e
; e ![\frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}} \frac{\partial I}{\partial L} = \frac{V}{R.\sqrt[2]{10}}.-\frac{1}{{L}^{2}}](/latexrender/pictures/336bcda187ceec6ab911e2912aaecf7d.png) .
.

 que depende de 3 variáveis
que depende de 3 variáveis  ,
, 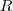 e
e  as quais dependem do tempo
as quais dependem do tempo  . Assim, a derivada total de
. Assim, a derivada total de 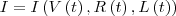
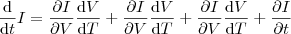 .
.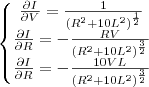
 no instante indicado, para que a corrente se mantenha constante, isto é,
no instante indicado, para que a corrente se mantenha constante, isto é, 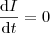 , então basta substituir na relação da derivada e teremos um resultado. Veja que no instante indicado temos
, então basta substituir na relação da derivada e teremos um resultado. Veja que no instante indicado temos