 por Kabection » Dom Jul 14, 2013 00:40
por Kabection » Dom Jul 14, 2013 00:40
Olá a todos, estava tentando resolver essa questão que a princípio achei fácil, mas depois de pensar um pouco mais, não cheguei a conclusão final.
O enunciado é:
1) Determinar se o seguinte conjunto é subespaço de R³: W = { (a1,a2,a3) | a1=3a2 e a3=-a2 }
Minha resposta foi:
R = W não é subespaço pois, pela propriedade 2 de subespaço, u + v pertence a W. Já para esse caso:
Dados u,v pertencentes a W => u = ( 3(a2), (a1)/3 , -(a1)/3 ) e v = ( 3(b2) , (b1)/3 , -(b1)/3 ) => u+v = (3(a2+b2) , (a1+b1)/3 , -(a1+b1)/3 ) .
Gostaria de saber, se pelo fato de o sistema não ser determinado, o W não poderia ser subespaço vetorial, pois nesse caso a2 = a1/3 e também a2 = -a3
Agradeço a atenção.
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por e8group » Dom Jul 14, 2013 12:41
por e8group » Dom Jul 14, 2013 12:41
Acho mais fácil reescrever o conjunto dado da seguinte forma
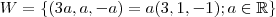
(por simplicidade troquei "a_2 " por "a" ) que é o cojunto de todos os múltiplos de

.Afirmamos que

é subespaço do

.De fato :
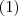
Designando

o vetor nulo do

. Claramente ,

(deixo a cargo de você demonstrar isto)

Dados
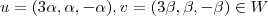
.Temos :
![u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W](/latexrender/pictures/5feea62479765446c0b7bcb1cba9d534.png)
.
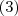
Agora basta mostrar que para todo escalar

e vetor
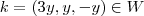
tem-se
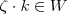
.Tente fazer !!
OBS.: O sistema que você mencionou é possível e indeterminado .Isto já era de ser esperado .Como vemos em (2) ,

não exprimir-se de forma única como

. Pondo

,para cada escolha arbitrária

, obtemos um novo número

que somado a

resulta

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Kabection » Seg Jul 15, 2013 00:00
por Kabection » Seg Jul 15, 2013 00:00
Obrigado santhiago . Realmente o que estava me confundindo foi esse sistema, mas desse jeito que você fez (reescrevendo o sistema) ficou bem mais claro e fácil de resolver essa questão. Vlw msm.
Completando a resposta:
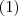
Designando

o vetor nulo do

. Claramente ,

, pois quando


Provado acima ^
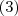
Agora basta mostrar que para todo escalar

e vetor
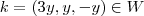
tem-se

,
para todo

e


Logo W é subespaço vetorial de
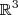
.
-
Kabection
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Seg Jan 16, 2012 15:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Ciência da Computação
- Andamento: cursando
 por e8group » Seg Jul 15, 2013 10:28
por e8group » Seg Jul 15, 2013 10:28
Não há de quê .Está correto .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Linear
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Álgebra Linear][Dúvida][Provar subespaço]
por Nicolas1Lane » Sex Set 12, 2014 16:45
- 1 Respostas
- 2107 Exibições
- Última mensagem por adauto martins

Qui Out 23, 2014 15:11
Álgebra Linear
-
- (Unesp) sistema linear questão 36
por lnd_rj1 » Dom Fev 10, 2013 09:09
- 0 Respostas
- 1513 Exibições
- Última mensagem por lnd_rj1

Dom Fev 10, 2013 09:09
Álgebra Linear
-
- SISTEMA LINEAR DÚVIDA
por Fernanda Lauton » Qui Jun 10, 2010 19:43
- 4 Respostas
- 3337 Exibições
- Última mensagem por MarceloFantini

Sáb Jun 12, 2010 12:37
Sistemas de Equações
-
- Sistema Linear - Dúvida
por Veronica » Seg Abr 23, 2012 22:34
- 0 Respostas
- 1149 Exibições
- Última mensagem por Veronica

Seg Abr 23, 2012 22:34
Sistemas de Equações
-
- [Sistema linear dúvida]
por Aprendiz2012 » Dom Ago 26, 2012 21:26
- 1 Respostas
- 1612 Exibições
- Última mensagem por MarceloFantini

Dom Ago 26, 2012 22:57
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


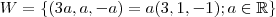 (por simplicidade troquei "a_2 " por "a" ) que é o cojunto de todos os múltiplos de
(por simplicidade troquei "a_2 " por "a" ) que é o cojunto de todos os múltiplos de  .Afirmamos que
.Afirmamos que  é subespaço do
é subespaço do  .De fato :
.De fato : 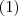
 o vetor nulo do
o vetor nulo do  (deixo a cargo de você demonstrar isto)
(deixo a cargo de você demonstrar isto)  Dados
Dados 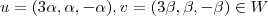 .Temos :
.Temos : ![u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W u+v = (3\alpha + 3\beta , \alpha +\beta , - \alpha - \beta ) = (3(\alpha + \beta) ,\alpha +\beta, -(\alpha + \beta)) =\\ \underbrace{[\alpha + \beta]}_{\in \mathbb{R}}]\cdot (3,1,-1) \in W](/latexrender/pictures/5feea62479765446c0b7bcb1cba9d534.png) .
. 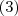 Agora basta mostrar que para todo escalar
Agora basta mostrar que para todo escalar  e vetor
e vetor 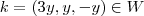 tem-se
tem-se 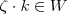 .Tente fazer !!
.Tente fazer !! não exprimir-se de forma única como
não exprimir-se de forma única como  . Pondo
. Pondo  ,para cada escolha arbitrária
,para cada escolha arbitrária  , obtemos um novo número
, obtemos um novo número  que somado a
que somado a 

 ,
, 

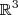 .
.