 por ma-mine » Sáb Jul 13, 2013 15:24
por ma-mine » Sáb Jul 13, 2013 15:24
considere a função real de variável real w'(w)=x.lnx
Determine w(x) sabendo que w(1)=0
Alguem me saberá ajudar nesta questão?
-
ma-mine
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jul 13, 2013 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em gestão de empresas
- Andamento: cursando
 por young_jedi » Dom Jul 14, 2013 11:54
por young_jedi » Dom Jul 14, 2013 11:54
A equação é

ou
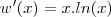
?
se for a segunda é so realizar a integral
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por ma-mine » Dom Jul 14, 2013 15:54
por ma-mine » Dom Jul 14, 2013 15:54
a equação é w'(x)
e já agora, não a outra maneira de resolver sem utilizar a integral?
-
ma-mine
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Sáb Jul 13, 2013 15:15
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em gestão de empresas
- Andamento: cursando
 por e8group » Dom Jul 14, 2013 19:00
por e8group » Dom Jul 14, 2013 19:00
Se permite-me participar da conversar ,caso você ainda não aprendeu técnicas de integração.Alternativamente, o que podemos fazer é pensar em uma função que sua derivada é
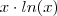
.Neste caso é fácil determinar tal função . Comece observando que a função
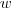
é dada por

onde
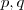
são polinômios . Derivando então
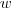
em ordem a

, obtemos :
![w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x) w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x)](/latexrender/pictures/54017cc431f24f051634d6daf0b0033f.png)
. Comparando a igualdade ,só podemos ter ,

e
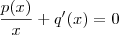
.Assim , fica fácil ver que

(Por quê ? ) e portanto ,

;donde segue

onde

é uma constante (pois,

) . Assim, a função
é definida por :
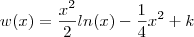
. Agora basta usar que
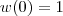
para determinar k .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Derivadas] como calcular
por ghiza » Dom Jul 14, 2013 21:45
- 2 Respostas
- 1766 Exibições
- Última mensagem por Man Utd

Dom Jul 14, 2013 23:39
Cálculo: Limites, Derivadas e Integrais
-
- Como calcular derivadas com a constante "e"
por fer_carnie » Seg Jun 20, 2011 20:40
- 1 Respostas
- 2085 Exibições
- Última mensagem por Fabio Cabral

Seg Jun 20, 2011 22:22
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] Dificuldade para calcular derivadas CDI 1
por srmai » Seg Nov 04, 2013 01:21
- 0 Respostas
- 2261 Exibições
- Última mensagem por srmai

Seg Nov 04, 2013 01:21
Cálculo: Limites, Derivadas e Integrais
-
- (derivadas) derivadas com raiz como se faz
por jana garcia » Qua Jun 25, 2014 00:28
- 1 Respostas
- 2963 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 01:13
Cálculo: Limites, Derivadas e Integrais
-
- [Derivadas] calcular os intervalos de f(x)
por JessyBr » Qui Mar 29, 2012 00:46
- 2 Respostas
- 1855 Exibições
- Última mensagem por LuizAquino

Qui Mar 29, 2012 12:41
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




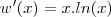


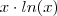 .Neste caso é fácil determinar tal função . Comece observando que a função
.Neste caso é fácil determinar tal função . Comece observando que a função 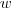 é dada por
é dada por onde
onde 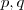 são polinômios . Derivando então
são polinômios . Derivando então 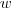 em ordem a
em ordem a  , obtemos :
, obtemos : ![w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x) w'(x) = [p(x)\cdot ln(x) + q(x)]' = p'(x) \cdot ln(x) + \frac{p(x)}{x} + q'(x) = x \cdot ln(x)](/latexrender/pictures/54017cc431f24f051634d6daf0b0033f.png) . Comparando a igualdade ,só podemos ter ,
. Comparando a igualdade ,só podemos ter ,  e
e 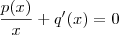 .Assim , fica fácil ver que
.Assim , fica fácil ver que  (Por quê ? ) e portanto ,
(Por quê ? ) e portanto ,  ;donde segue
;donde segue  onde
onde  é uma constante (pois,
é uma constante (pois, ) . Assim, a função
) . Assim, a função 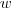 é definida por :
é definida por : 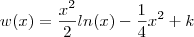 . Agora basta usar que
. Agora basta usar que 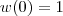 para determinar k .
para determinar k .


 , avisa que eu resolvo.
, avisa que eu resolvo.

