 por felipexxavier » Seg Mar 31, 2008 11:38
por felipexxavier » Seg Mar 31, 2008 11:38
O exercício é da matéria de trigonometria...
De um ponto A, no solo, visam-se a base B e o Topo C de um bastão colocado verticalmente no alto de uma colina, sob ângulos de 30° e 45° respectivamente. Se o bastão mede 4m de comprimento, calcule a altura da colina, em metros.
fiz sobre a tg de 45° que seria co/ca mas o resultado dá quebrado tipo 5,46, tenho dificuldades no exercício.
-
felipexxavier
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 31, 2008 11:24
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Mar 31, 2008 13:11
por admin » Seg Mar 31, 2008 13:11
Olá, seja bem-vindo!
Comente os passos que você seguiu para obter este resultado, assim poderemos discutir melhor.
De qualquer forma, provavelmente sua idéia esteja correta porque eu encontrei

metros para a altura da colina que corresponde ao seu valor aproximado.
Vamos chamar de O o ponto no solo, alinhado verticalmente com o bastão, na base da colina.
E x a altura OB que procuramos.
As curiosidades que eu tenho para entender melhor sua dificuldade são as seguintes:
-Fez o desenho? Alguma dúvida nele?
-Visualizou o triângulo AOC retângulo em O?
-E o mais importante: percebeu que ele também é isósceles, sendo que os catetos AO e OC medem 4+x?
Com este desenho feito, utilizei a tangente de
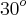
.
Comente suas dúvidas e poderemos conversar sobre elas.
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por felipexxavier » Seg Mar 31, 2008 16:00
por felipexxavier » Seg Mar 31, 2008 16:00
Fábio...
Fiz o desenho, mas como sou novo aqu,i ainda não aprendi (risos)...
Como o ângulo é de 45°, significa que o CA=CO.
Cheguei no CA= 4+x
Sabendo o CA, a formula da tg você descobre x.
CA30° = CA45°
tg30° = CO/CA ->> tg30° = x/x+4
Substituindo os valores você chega a esse resultado:
2 raiz de 3 + 2
Você colocou + 1
Ok?!
Assim:
De um ponto A, no solo, visam-se a base B e o Topo C de um bastão colocado verticalmente no alto de uma colina, sob ângulos de 30° e 45° respectivamente.
Se o bastão mede 4m de comprimento, calcule a altura da colina, em metros.
2 raiz de três +2 =
2.1,73 + 2 =
3,46 + 2 =
5,46
Resposta: A altura da colina é de 5 metros e 46 centímetros.
É isso mesmo,pq vc até comentou que seria um triangulo isoceles, mas só vejo retângulo.
-
felipexxavier
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 31, 2008 11:24
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Seg Mar 31, 2008 17:11
por admin » Seg Mar 31, 2008 17:11
Olá.
Coloquei +1 mesmo, note que 2 está em evidência, vou repetir aqui:

Esta sua afirmação não é verdadeira:
Como o ângulo é de 45°, significa que o CA=CO.
AC é a diagonal de um quadrado de lado AO=OC.
Ou seja,
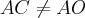
e
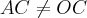
.
Como uma figura diz mais do que palavras, veja:

- triangulo_retangulo_isosceles.jpg (21.95 KiB) Exibido 16807 vezes
Repare que CO/CA que você citou é na verdade o seno de
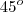
e não a tangente de
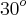
.
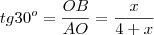

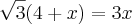
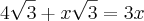
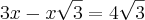


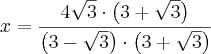
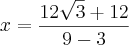

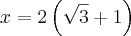
metros
OK?
Caso tenha alguma dúvida ou discorde de algo, por favor, comente conosco!
Até mais.
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por felipexxavier » Seg Mar 31, 2008 17:56
por felipexxavier » Seg Mar 31, 2008 17:56
Só tenho a agradecer.
Li o seu comentário para um rapaz, onde cita que não é um professor exatamente, apesar da licenciatura, porém vejo que tem potencial, parabéns e o melhor de tudo esse site tem um conteúdo muito rico, que esta de parabéns também!
Saibam que estarei todos os dias neste site e quais forem as dúvidas nas aulas de cálculo, algébra linear e física ou até mesmo algo novo, inovador sobre a nossa querida matemática, trarei para o fórum, muito obrigado!
Felipe Xavier
Technical Telecomunications
-
felipexxavier
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Seg Mar 31, 2008 11:24
- Área/Curso: Estudante
- Andamento: cursando
Voltar para Trigonometria
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Exercicio de Trigonometria
por Churchill » Sáb Out 02, 2010 19:16
- 2 Respostas
- 2373 Exibições
- Última mensagem por Churchill

Dom Out 03, 2010 07:51
Trigonometria
-
- [trigonometria] Exercício
por fff » Qua Abr 02, 2014 06:42
- 2 Respostas
- 1540 Exibições
- Última mensagem por fff

Qua Abr 02, 2014 10:33
Trigonometria
-
- Trigonometria: Exercício de concurso
por Celma » Seg Jul 01, 2013 19:02
- 2 Respostas
- 2200 Exibições
- Última mensagem por Celma

Seg Jul 01, 2013 20:27
Trigonometria
-
- [Dúvida em exercicio de Trigonometria] Ajuda pff
 por cristimd » Sáb Mai 04, 2013 14:41
por cristimd » Sáb Mai 04, 2013 14:41
- 1 Respostas
- 1360 Exibições
- Última mensagem por young_jedi

Dom Mai 05, 2013 09:56
Trigonometria
-
- [trigonometria] exercicio, me ajudem por favor?
por amanda s » Sex Nov 15, 2013 20:15
- 1 Respostas
- 7205 Exibições
- Última mensagem por nakagumahissao

Sáb Nov 16, 2013 00:50
Trigonometria
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 metros para a altura da colina que corresponde ao seu valor aproximado.
metros para a altura da colina que corresponde ao seu valor aproximado.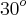 .
.

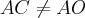 e
e 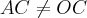 .
.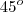 e não a tangente de
e não a tangente de 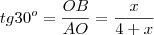

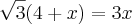
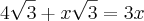
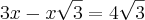


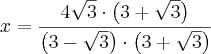
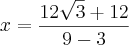

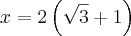 metros
metros




