 por Rafael16 » Qui Jun 20, 2013 13:36
por Rafael16 » Qui Jun 20, 2013 13:36
Olá, estou começando agora a estudar cálculo por conta própria, e vi a resolução do exercício abaixo, mas não entendi o porque que
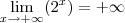
. Um número qualquer elevado ao infinito num seria indeterminação?
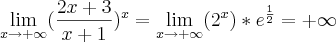
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
 por temujin » Qui Jun 20, 2013 13:47
por temujin » Qui Jun 20, 2013 13:47
Na verdade, uma indeterminação é algo que não te diz exatamente como o limite vai se comportar. Por exemplo, se vc tiver um limite nas formas
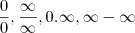
De imediato vc não consegue dizer como a função se comporta na região estudada.
No caso da sua função, uma base qualquer, constante, elevada a um número cada vez maior, cresce cada vez mais rápido. Faça uma tabelinha simples:
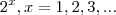
O que acontece com o valor da função?
-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
 por Rafael16 » Qui Jun 20, 2013 14:52
por Rafael16 » Qui Jun 20, 2013 14:52
Ah sim, entendi. Obrigado temujin!
-
Rafael16
- Colaborador Voluntário

-
- Mensagens: 154
- Registrado em: Qui Mar 01, 2012 22:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Análise de Sistemas
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
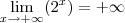 . Um número qualquer elevado ao infinito num seria indeterminação?
. Um número qualquer elevado ao infinito num seria indeterminação?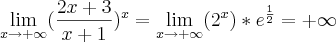

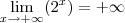 . Um número qualquer elevado ao infinito num seria indeterminação?
. Um número qualquer elevado ao infinito num seria indeterminação?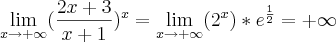

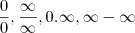
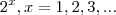


 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.