 por VenomForm » Qua Jun 19, 2013 13:57
por VenomForm » Qua Jun 19, 2013 13:57
Editado pela última vez por
VenomForm em Qui Jun 20, 2013 11:54, em um total de 1 vez.
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
 por VenomForm » Qui Jun 20, 2013 11:54
por VenomForm » Qui Jun 20, 2013 11:54
Dando 1 UP e corrigindo o resultado final
-
VenomForm
- Usuário Ativo

-
- Mensagens: 14
- Registrado em: Qua Fev 27, 2013 14:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Ciências da Computação
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx \int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx](/latexrender/pictures/59f152fc1330f669c380211f223790d3.png)
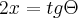
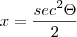
![\frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta \frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta](/latexrender/pictures/9b5cc58a7209758b9e525763e18999c2.png)
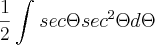
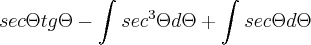
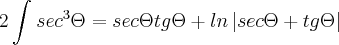
![\int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right] \int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right]](/latexrender/pictures/dd667609adb1cb1b7f3dc6d5fe9ef3bd.png)
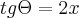
![sec\Theta=\sqrt[2]{1+4{x}^{2}} sec\Theta=\sqrt[2]{1+4{x}^{2}}](/latexrender/pictures/80e79e3b50f340d824c9ca4a616c6d81.png)
![\frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right] \frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right]](/latexrender/pictures/4786cbd03da47f7c1b7f149457c66c07.png)

![\int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx \int_{0}^{1}\sqrt[2]{1+4{x}^{2}}dx](/latexrender/pictures/59f152fc1330f669c380211f223790d3.png)
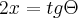
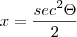
![\frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta \frac{1}{2}\int_{}^{}\sqrt[2]{1+{tg}^{2}\Theta}{sec}^{2}\Theta d\Theta](/latexrender/pictures/9b5cc58a7209758b9e525763e18999c2.png)
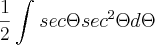
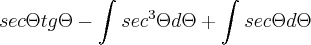
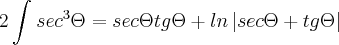
![\int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right] \int_{}^{}{sec}^{3}\Theta=\frac{1}{2}\left[sec\Theta tg\Theta+ln\left|sec\Theta+tg\Theta \right| \right]](/latexrender/pictures/dd667609adb1cb1b7f3dc6d5fe9ef3bd.png)
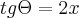
![sec\Theta=\sqrt[2]{1+4{x}^{2}} sec\Theta=\sqrt[2]{1+4{x}^{2}}](/latexrender/pictures/80e79e3b50f340d824c9ca4a616c6d81.png)
![\frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right] \frac{1}{4}\left[\sqrt[2]{1+4{x}^{2}}2x+ln\left|\sqrt[2]{1+4{x}^{2}}+2x \right| \right]](/latexrender/pictures/4786cbd03da47f7c1b7f149457c66c07.png)



 .
.



