 por temujin » Seg Jun 17, 2013 17:36
por temujin » Seg Jun 17, 2013 17:36
Olá pessoal.
Tô enroscado nesta questão.
Acho que tem que usar o Teorema fundamental do calculo, mas até agora não saiu, :evil:
Seja
![f:[0;1] \rightarrow \mathbb{R} f:[0;1] \rightarrow \mathbb{R}](/latexrender/pictures/153208225fa418aaca01c53b0e3a05f7.png)
uma função contínua tal que
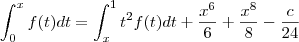
. Calcular o valor de c.
Alguma idéia??

-
temujin
- Usuário Parceiro

-
- Mensagens: 69
- Registrado em: Qui Mar 14, 2013 15:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Economia
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Teorema fundamental do calculo
por Thyago Quimica » Dom Jun 16, 2013 16:38
- 1 Respostas
- 1051 Exibições
- Última mensagem por e8group

Dom Jun 16, 2013 20:12
Cálculo: Limites, Derivadas e Integrais
-
- [Cálculo III] - Teorema de Stokes
por Feliperpr » Sáb Abr 21, 2012 16:08
- 5 Respostas
- 2630 Exibições
- Última mensagem por Feliperpr

Sáb Abr 21, 2012 19:33
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Calculo de limite usando o teorema do confronto.
por erickm93 » Qua Mai 22, 2013 10:48
- 3 Respostas
- 6019 Exibições
- Última mensagem por erickm93

Qua Mai 22, 2013 23:49
Cálculo: Limites, Derivadas e Integrais
-
- Calculo vetorial, integrais de linha e Teorema de green
 por Fernandobertolaccini » Qui Jun 11, 2015 20:19
por Fernandobertolaccini » Qui Jun 11, 2015 20:19
- 0 Respostas
- 2303 Exibições
- Última mensagem por Fernandobertolaccini

Qui Jun 11, 2015 20:19
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] calculo de integral - coordenada esferica
por fatalshootxd » Ter Mar 31, 2015 00:43
- 1 Respostas
- 4526 Exibições
- Última mensagem por adauto martins

Sáb Abr 04, 2015 16:13
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 14 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![f:[0;1] \rightarrow \mathbb{R} f:[0;1] \rightarrow \mathbb{R}](/latexrender/pictures/153208225fa418aaca01c53b0e3a05f7.png) uma função contínua tal que
uma função contínua tal que 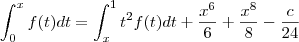 . Calcular o valor de c.
. Calcular o valor de c.

![f:[0;1] \rightarrow \mathbb{R} f:[0;1] \rightarrow \mathbb{R}](/latexrender/pictures/153208225fa418aaca01c53b0e3a05f7.png) uma função contínua tal que
uma função contínua tal que 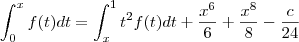 . Calcular o valor de c.
. Calcular o valor de c.


![\frac{d}{dx} \left [\int_0^x f(t)dt \right ] = \frac{d}{dx} \left [\int_x^1 t^2f(t)dt +\frac{x^6}{6}+\frac{x^8}{8}-\frac{c}{24}\right ] \frac{d}{dx} \left [\int_0^x f(t)dt \right ] = \frac{d}{dx} \left [\int_x^1 t^2f(t)dt +\frac{x^6}{6}+\frac{x^8}{8}-\frac{c}{24}\right ]](/latexrender/pictures/1c4de75dcb5fabbdb6ce6fcb682557eb.png)
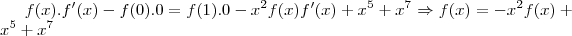
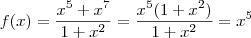
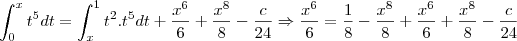
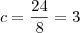


 .
.



