Penso que W . 2a = 0 e W . (a -b) = 0
Logo
(x,y,z) . (-2,4,6) nos dá
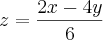
(x,y,z) . (-3,2,4) nos dá x=
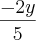.Isolando pra cá e pra lá, chego a (-2y/5, y, -4y/5).
Dúvida. O que faço para achar valor de Y???
por dehcalegari » Seg Mai 13, 2013 17:34
.
por e8group » Sáb Jun 15, 2013 10:41
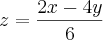
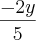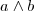é simultaneamente ortogonal a 
.Se você utilizar o dispositivo prático para calcular o produto misto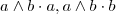 
verá que uma linha da matriz é múltipla da outra resultando 
.
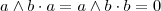Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
o ângulo entre o eixo horizontal e o afixo 
. O triângulo é retângulo com catetos 
e 
, tal que 
. Seja 
o ângulo complementar. Então 
. Como 
, o ângulo que o afixo 
formará com a horizontal será , mas negativo pois tem de ser no quarto quadrante. Se 
, então 
. Como módulo é um: 
.
.