Olá pessoal, estou com um problema aqui que não consigo resolver.
O velocimetro de um automóvel registra a velocidade de 50km/h quando ele passa por um marco quilométrico ao longo da rodovia. Quatro minutos mais tarde, quando o automóvel passa por um segundo marco a 5 Km do primeiro, o velocimetro registra 55Km/h. Use o teorema do valor médio para provar que a velocidade excedeu a 70 Km/h em alguns instântes enquanto o automovel percorria a distância entre os dois marcos.
Primeiramente eu tentei criar um gráfico do tempo em função da velocidade e apliquei na fórmula do valor médio
f '(c) = f(b) - f(a)/ b - a
quando o tempo é 4 a velocidade é 55, logo f(4) = 55
quando o tempo é 0 a velocidade é 50, logo f(0)= 50
f '(c) = 55 - 50 / 4 - 0
f '(c) = 5/4
Apartir deste ponto já não sei o que posso fazer =/. Outro problema é que não sei aonde posso usar a distância de 5 Km entre os marcos.
Obrigado desde já.


 na variável
na variável  que fornece a posição do automóvel .Suponha que no instante
que fornece a posição do automóvel .Suponha que no instante 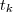 ,tem-se
,tem-se 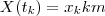 para algum
para algum 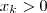 e
e 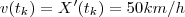 ,mas sabemos que após 4 min ,
,mas sabemos que após 4 min , 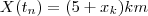 com
com 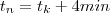 (pois
(pois 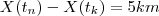 ) .Mas ,pelo TVM , existe algum
) .Mas ,pelo TVM , existe algum  em
em 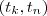 tal que ,
tal que ,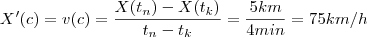 .
.
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)