Questão de decibel.

[Arthur_Bulcao]

Minha questão é "simples":
O Nível de pressão sonora (L) é "dado" em decibel (dB). E a fórmula pra calculá-lo (apartir de p, que é pressão sonora) se dá por:

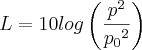, onde

Por ser logarítmico, não dá pra dizer por exemplo, que 50 dB + 50 dB = 100 dB.
Porém há uma relação para esse tipo de soma. Pode-se dizer que



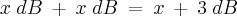
No entanto eu não sei como provar isso. Essa é a questão. Como se faz pra prová-lo?



Se for de ajuda, tenho que

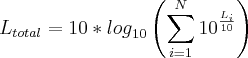, onde é a N somas de vários L (no caso talvez poderia ser tratado L+L... sei lá...).








[i]PS: Sinto-me na obrigação de dizer que dB NÃO É UNIDADE de nível de pressão sonora. É uma pseudounidade, afinal não se utiliza unidade em 'níveis'.