 por LucasSG » Qui Jun 06, 2013 22:45
por LucasSG » Qui Jun 06, 2013 22:45
Escreva uma equação vetorial da reta r concorrente com s, paralela ao plano pi, e perpendicular a reta AB. São dados pi: 2x-y+3z-1=0, A=(1,0,1), B=(0,1,2), s: X=(4,5,0)+a(3,6,1)
Não consigo resolver esse exercício, eu sei de algumas coisas:
Se r é paralela ao plano pi, ela é ortogonal ao vetor (2,-1,3), que é o vetor normal ao plano pi. Logo o produto escalar de r com (2,-1,3) sendo r o vetor diretor de r tem que ser nulo.
Se r é perpendicular a reta AB, então r.(-1,1,1)=0 (o produto escalar do vetor diretor da reta r com o vetor AB tem que ser nulo.)
Mas se eu escrevo a reta r na forma: X=(a,b,c)+y(m,n,p), eu tenho 7 incognitas nessa equação, e mesmo resolvendo os sistemas anteriores ainda me sobrariam varias, não sei bem como posso usar as informações de que r é concorrente com r e perpendicular a reta AB. (Eu acredito que tenho que encontrar os pontos onde as retas se interceptam, mas não sei como isso vai me ajudar, já que eu adicionaria varios parametros das outras retas ao sistema).
Por favor, podem me ajudar a prosseguir com a resolução?
Obrigado.
-
LucasSG
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 22, 2013 08:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por e8group » Sáb Jun 08, 2013 22:15
por e8group » Sáb Jun 08, 2013 22:15
Seguindo seu raciocínio , seja
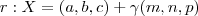
.
Se
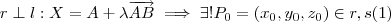
e
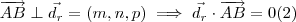
.
Se
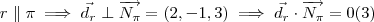
. Por
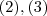
teremos um sistema de três incógnitas para 2 equações ,poderemos por exemplo escrever
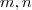
em função de

.Assim , o conjunto dos vetores múltiplos de

é o conjunto dos vetores diretores de

,portanto a escolha para

é arbitrária .
Se

são concorrentes,então ambas retas possuem um único ponto em comum (4) .Suponha que
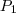
seja este ponto .Tente utilizar (4) e (1) para concluir .Comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica]Equação da Reta
por IlgssonBraga » Ter Nov 05, 2013 14:34
- 1 Respostas
- 1626 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 12:25
Geometria Analítica
-
- geometria analítica estudo da reta distancia do ponta à reta
por jeffersonricardo » Dom Ago 22, 2010 08:29
- 1 Respostas
- 2418 Exibições
- Última mensagem por Pedro123

Seg Ago 23, 2010 22:24
Geometria Analítica
-
- [reta] geometria analítica
 por Leidiana Catum » Seg Jul 14, 2008 00:06
por Leidiana Catum » Seg Jul 14, 2008 00:06
- 1 Respostas
- 11920 Exibições
- Última mensagem por admin

Seg Jul 14, 2008 02:34
Geometria Analítica
-
- geometria analítica estudo da reta
por jeffersonricardo » Dom Ago 22, 2010 08:22
- 0 Respostas
- 1296 Exibições
- Última mensagem por jeffersonricardo

Dom Ago 22, 2010 08:22
Geometria Analítica
-
- [Geometria Analítica] Encontrar a reta t
por -civil- » Ter Ago 09, 2011 21:49
- 1 Respostas
- 2211 Exibições
- Última mensagem por LuizAquino

Qui Ago 11, 2011 23:31
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


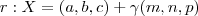 .
.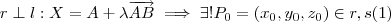 e
e 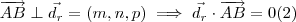 .
.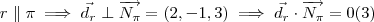 . Por
. Por 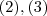 teremos um sistema de três incógnitas para 2 equações ,poderemos por exemplo escrever
teremos um sistema de três incógnitas para 2 equações ,poderemos por exemplo escrever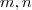 em função de
em função de  .Assim , o conjunto dos vetores múltiplos de
.Assim , o conjunto dos vetores múltiplos de  ,portanto a escolha para
,portanto a escolha para  são concorrentes,então ambas retas possuem um único ponto em comum (4) .Suponha que
são concorrentes,então ambas retas possuem um único ponto em comum (4) .Suponha que 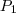 seja este ponto .Tente utilizar (4) e (1) para concluir .Comente as dúvidas .
seja este ponto .Tente utilizar (4) e (1) para concluir .Comente as dúvidas .





