Por favor não poste a resolução, só me ajuda entrar no caminho do resultado (:
A questão é...
Se um arco de 60º num circulo I tem o mesmo comprimento de um arco de 40º num circulo II, então, a razão da área do circulo I pela área do circulo II é:
Bom fiz os calculos e até agora só consigo chegar no valor da circunferência
que é 3/2, eu acho.
Circulo I
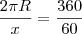
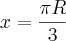
Circulo II
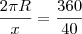
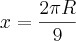
com isso a circunferência vale...
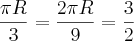
Daí em diante já fiz várias tentativas mas nunca consigo chegar no resultado que é 4/9.




![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)