 por LucasSG » Dom Jun 02, 2013 22:21
por LucasSG » Dom Jun 02, 2013 22:21
A piramide da figura tem por base um quadrado de lado 2. As arestas que contem o vertice V formam angulos de 45 com o plano do quadrado, e a base (

é positiva

Calcule
![[\vec{DC}, \vec{DA}/2, \vec{DV}] [\vec{DC}, \vec{DA}/2, \vec{DV}]](/latexrender/pictures/214c0245206bfc5d34f041898cd74e10.png)
(produto misto destes três vetores)
Bom, pra calcular o produto misto eu fiz (IIDCII*IIDA/2II*Sen(x))*IIDVII*cos(y)
Onde x é o angulo entre DC E DA e y o angulo entre o produto vetorial de DC e DA e DV.
O resultado obtido foi
![2.\sqrt[]{2} 2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png)
Mas o resultado do exercicio é
![-2.\sqrt[]{2} -2.\sqrt[]{2}](/latexrender/pictures/cd4c2d00aae30be84198313e10fdecf1.png)
Gostaria de ajuda pra saber onde eu errei na resolução.
Obrigado.
-
LucasSG
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 22, 2013 08:26
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por LuizAquino » Sex Jun 07, 2013 17:49
por LuizAquino » Sex Jun 07, 2013 17:49
LucasSG escreveu:A piramide da figura tem por base um quadrado de lado 2. As arestas que contem o vertice V formam angulos de 45 com o plano do quadrado, e a base (

é positiva

- figura.png (28.08 KiB) Exibido 2389 vezes
Calcule
![[\vec{DC}, \vec{DA}/2, \vec{DV}] [\vec{DC}, \vec{DA}/2, \vec{DV}]](/latexrender/pictures/214c0245206bfc5d34f041898cd74e10.png)
(produto misto destes três vetores)
Bom, pra calcular o produto misto eu fiz (IIDCII*IIDA/2II*Sen(x))*IIDVII*cos(y)
Onde x é o angulo entre DC E DA e y o angulo entre o produto vetorial de DC e DA e DV.
O resultado obtido foi
![2.\sqrt[]{2} 2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png)
Mas o resultado do exercicio é
![-2.\sqrt[]{2} -2.\sqrt[]{2}](/latexrender/pictures/cd4c2d00aae30be84198313e10fdecf1.png)
Gostaria de ajuda pra saber onde eu errei na resolução.
Obrigado.
Use a Regra da Mão Direita e responda o seguinte: qual é o sentido do vetor

? Depois de aplicar esta regra, você deve concluir que o ângulo y entre este vetor e
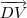
é 135°. Considerando esta informação, tente concluir o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4945 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- Produto Misto
por Felipe Ferraiol » Sex Jun 03, 2011 01:01
- 1 Respostas
- 2668 Exibições
- Última mensagem por LuizAquino

Sex Jun 03, 2011 09:43
Geometria Analítica
-
- [PRODUTO MISTO]
por LUAN UFPE » Qua Fev 27, 2013 15:58
- 1 Respostas
- 2102 Exibições
- Última mensagem por LUAN UFPE

Qua Fev 27, 2013 17:42
Geometria Analítica
-
- [Produto Misto] Geometria Analítica
 por Thamiires » Sex Dez 02, 2011 21:27
por Thamiires » Sex Dez 02, 2011 21:27
- 1 Respostas
- 1872 Exibições
- Última mensagem por TheoFerraz

Sáb Dez 03, 2011 10:14
Geometria Analítica
-
- [Produto Misto] VOLUME DO PARALELEPIPEDO
por ubelima » Qua Mai 16, 2012 20:27
- 1 Respostas
- 4288 Exibições
- Última mensagem por LuizAquino

Sáb Mai 19, 2012 15:45
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é positiva
é positiva
![[\vec{DC}, \vec{DA}/2, \vec{DV}] [\vec{DC}, \vec{DA}/2, \vec{DV}]](/latexrender/pictures/214c0245206bfc5d34f041898cd74e10.png) (produto misto destes três vetores)
(produto misto destes três vetores)![2.\sqrt[]{2} 2.\sqrt[]{2}](/latexrender/pictures/ddf6c53cdaf7bbc107f4017b1175e22f.png)
![-2.\sqrt[]{2} -2.\sqrt[]{2}](/latexrender/pictures/cd4c2d00aae30be84198313e10fdecf1.png)


 ? Depois de aplicar esta regra, você deve concluir que o ângulo y entre este vetor e
? Depois de aplicar esta regra, você deve concluir que o ângulo y entre este vetor e 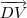 é 135°. Considerando esta informação, tente concluir o exercício.
é 135°. Considerando esta informação, tente concluir o exercício.

 .
.



