[Algebra Linear] Sistema

por **fabriel** » Dom Jun 02, 2013 03:44

É ai pessoal, blz? Então estou com uma duvida num exercicio aqui.
Veja o exercicio:

Determinar os valores de m para os quais o sistema descrito abaixo é possivel e determiado:

x+2y-2z-t=1

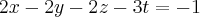
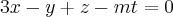
Resolvendo.
A matriz ampliada associada ao sistema é:
$\begin{pmatrix} 1 & 2 & -2 & -1 & 1 \\ 2 & -2 & -2 & -3 & -1 \\ 2 & -2 & -1 & -5 & 9 \\ 3 & -1 & 1 & -m & 0 \end{pmatrix}$

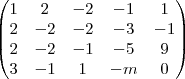
E fazendo umas operações elementares para resolvermos pelo metodo de Gauss chegamos nessa matriz:

$\begin{pmatrix} 1 & 2 & -2 & -1 & 1 \\ 0 & 1 & -\frac{1}{3} & \frac{1}{6} & \frac{1}{2} \\ 0 & 0 & 1 & -2 & 10 \\ 0 & 0 & 0 & \frac{81}{6}-m & \frac{1}{2} \end{pmatrix}$

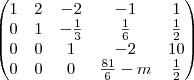
Deu pra entender né?

Mas ai não consigo resolver mais, preciso achar m, mas como, esta incógnita esta me levando a outras..

Obrigado

por **e8group** » Dom Jun 02, 2013 12:34

Considere a matriz aumentada [A|B]

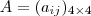associada ao sistema que você postou .Para este sistema ser possível e determinado a matriz $A =(a_{ij})_{4\times4}$ deve ser equivalente por linhas a matriz I_4

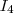(ou seja, existe um número finito de operações elementares que aplicado a

chega-se a I_4

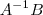) ,assim , a única solução é $A^{-1}B$ do sistema ,mas para que a matriz

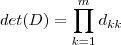seja invertível tem-se obrigatoriamente $det(A) \neq 0$ (pois $det(A^{-1} \cdot A) = det(A^{-1}) \cdot det(A) = det(I_4) = 1 \implies det(A) \neq 0$ ) . Usando que em uma matriz triangular $D = (d_{ij})_{m \times m} (i,j = 1,\hdots,m)$ seu determinante é dado por $det(D) = \prod_{k=1}^{m} d_{kk}$ ,temos que $det(A) = 1 \cdot 1 \cdot 1 \cdot (81/6 - m) \neq 0$ ,logo $m \neq 81/6$ .

por **fabriel** » Dom Jun 02, 2013 13:46

hummm, Obrigado. Quer dizer então que eu não poderia resolver esse problema sem os conhecimentos de determinantes e matriz inversa?

por **e8group** » Dom Jun 02, 2013 14:10

fabriel escreveu:hummm, Obrigado. Quer dizer então que eu não poderia resolver esse problema sem os conhecimentos de determinantes e matriz inversa?

Não é necessário . Observe a última matriz que você postou ,na última linha dela tiramos que (81/9 -m)t = 1/2

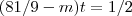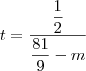para esta igualdade ser satisfeita devemos impor $(81/6 - m) \neq 0$ (pois,caso contrário 0 = 1/2 absurdo !) .Logo , $t =\frac{\dfrac{1}{2}}{\dfrac{81}{9}-m}$ .Na terceira linha da matriz vamos conseguir escrever

em função de $t =\frac{\dfrac{1}{2}}{\dfrac{81}{9}-m}$ ,disso obtemos uma solução para

.Pelo mesmo raciocínio vamos conseguir obter

e

. Você pode então concluir que fixado $m \neq 81/6$ o sistema será possível determinado .

por **e8group** » Dom Jun 02, 2013 14:19

Só para verificar a resposta :

http://www.wolframalpha.com/input/?i=%2 ... 9+%21%3D+0

[Algebra Linear] Sistema

[Algebra Linear] Sistema

[Algebra Linear] Sistema

Re: [Algebra Linear] Sistema

Re: [Algebra Linear] Sistema

Re: [Algebra Linear] Sistema

Re: [Algebra Linear] Sistema

Quem está online