 por Lenin » Sex Mai 31, 2013 03:10
por Lenin » Sex Mai 31, 2013 03:10
Pessoal, estou com dificuldades em resolver essa função:
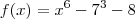
o resultado dela é 2 e -1.. eu consigo responder quando é elevado a quarta tipo essa:

que os zeros são 2, -1, 1 e -2..trocando o

por outra incógnita tipo
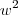
..mas com
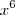
não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por e8group » Sex Mai 31, 2013 14:43
por e8group » Sex Mai 31, 2013 14:43
Por favor ,confirma se as funções são
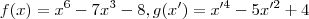
.Caso sejam ,podemos fazer
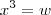
e

(Por quê ?) Assim ,

e

.
Ambas expressões podem ser calculadas pela fórmula resolvente .Tente concluir .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Lenin » Sex Mai 31, 2013 23:49
por Lenin » Sex Mai 31, 2013 23:49
santhiago escreveu:Por favor ,confirma se as funções são
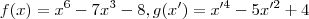
.Caso sejam ,podemos fazer
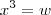
e

(Por quê ?) Assim ,

e

.
Ambas expressões podem ser calculadas pela fórmula resolvente .Tente concluir .
não entendi muito..
É tipo assim brother: eu fiz assim:
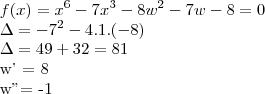
a partir dai não sei o que fazer.. como a resposta é x = 2 e 1, eu presumo que pego o w = 8 e faço
![{x}^{3} = 8
x = \sqrt[3]{8} = 2 {x}^{3} = 8
x = \sqrt[3]{8} = 2](/latexrender/pictures/b30ff66eecb340ed6150a37453d30c43.png)
só que como o w" = -1, não ha raiz real, só imaginária, ou
![x = \sqrt[3]{-1} = 1 x = \sqrt[3]{-1} = 1](/latexrender/pictures/6c37998a534d7ac1ebce45e28aa97d5a.png)
? há alguma regra para índice ímpar com radicando -1 seja igual a 1?
só vejo assim para o que eu achei coincide com o gabarito .
-
Lenin
- Usuário Dedicado

-
- Mensagens: 29
- Registrado em: Qua Abr 10, 2013 23:08
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Cursinho
- Andamento: cursando
 por e8group » Sáb Jun 01, 2013 12:30
por e8group » Sáb Jun 01, 2013 12:30
Note que
![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png)
,pois ,
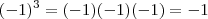
.Além disso ,

.Comente as dúvidas .
Observação :
Quando o índice

é impar e o radicando

é negativo ,o número é
![\sqrt[n]{a} < 0 \sqrt[n]{a} < 0](/latexrender/pictures/261ff9994999d43972a2ad6e6aa7238e.png)
é real ,casso fosse

par ,
![\sqrt[n]{a} \notin \mathbb{R} \sqrt[n]{a} \notin \mathbb{R}](/latexrender/pictures/94826bbc3ed30a99672afbb1ec6cfacd.png)
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Zeros da funcao
por sergiosilva » Qua Jan 05, 2011 22:59
- 3 Respostas
- 3863 Exibições
- Última mensagem por MarceloFantini

Qui Jan 06, 2011 21:13
Funções
-
- determinar os zeros da função
por anamendes » Dom Abr 29, 2012 12:37
- 1 Respostas
- 5815 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 14:06
Trigonometria
-
- Determinar os zeros da sequinte função
por franciscokael » Qui Out 21, 2010 15:36
- 2 Respostas
- 1898 Exibições
- Última mensagem por Elcioschin

Qui Out 28, 2010 17:07
Funções
-
- Dada uma função, calcular os zeros
por Tixa11 » Sáb Nov 10, 2012 12:26
- 4 Respostas
- 2942 Exibições
- Última mensagem por Tixa11

Seg Nov 12, 2012 18:05
Funções
-
- Descobrir zeros
por Tixa11 » Qui Jan 24, 2013 19:17
- 2 Respostas
- 1648 Exibições
- Última mensagem por Tixa11

Sex Jan 25, 2013 20:30
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
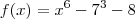

 por outra incógnita tipo
por outra incógnita tipo 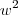 ..mas com
..mas com 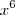 não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.
não estou conseguindo..ja troquei, achei os zeros, substitui na equação achei outros zeros para poder finalmente substituir novamente para poder achar os zeros da função primogênita..mas nada..agradecido desde já.

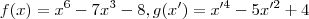 .Caso sejam ,podemos fazer
.Caso sejam ,podemos fazer 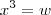 e
e  (Por quê ?) Assim ,
(Por quê ?) Assim ,  e
e  .
.
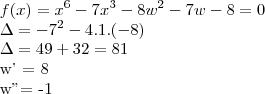
![{x}^{3} = 8
x = \sqrt[3]{8} = 2 {x}^{3} = 8
x = \sqrt[3]{8} = 2](/latexrender/pictures/b30ff66eecb340ed6150a37453d30c43.png)
![x = \sqrt[3]{-1} = 1 x = \sqrt[3]{-1} = 1](/latexrender/pictures/6c37998a534d7ac1ebce45e28aa97d5a.png) ? há alguma regra para índice ímpar com radicando -1 seja igual a 1?
? há alguma regra para índice ímpar com radicando -1 seja igual a 1?![\sqrt[3]{-1} = -1 \sqrt[3]{-1} = -1](/latexrender/pictures/ab94d7a2bd8fc931fd4e098fc8ae5dc2.png) ,pois ,
,pois , 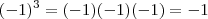 .Além disso ,
.Além disso ,  .Comente as dúvidas .
.Comente as dúvidas . é impar e o radicando
é impar e o radicando  é negativo ,o número é
é negativo ,o número é ![\sqrt[n]{a} < 0 \sqrt[n]{a} < 0](/latexrender/pictures/261ff9994999d43972a2ad6e6aa7238e.png) é real ,casso fosse
é real ,casso fosse ![\sqrt[n]{a} \notin \mathbb{R} \sqrt[n]{a} \notin \mathbb{R}](/latexrender/pictures/94826bbc3ed30a99672afbb1ec6cfacd.png) .
.

 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.