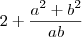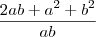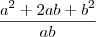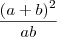por wgf » Ter Mai 28, 2013 21:03
-
wgf
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Qua Mai 15, 2013 18:52
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
por Molina » Ter Mai 28, 2013 22:48
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-
Molina
- Colaborador Moderador - Professor
-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatoração de uma expressão aparentemente irracional
por PeterHiggs » Qui Mai 31, 2012 10:15
- 2 Respostas
- 1670 Exibições
- Última mensagem por PeterHiggs
Qui Mai 31, 2012 21:45
Álgebra Elementar
-
- Fração equivalente
por jrmaialds » Qui Dez 06, 2012 14:52
- 1 Respostas
- 1352 Exibições
- Última mensagem por e8group
Qui Dez 06, 2012 16:31
Aritmética
-
- DUVIDA - URGENTE (tx de juros equivalente)
por Lobato » Sex Fev 04, 2011 22:17
- 0 Respostas
- 1184 Exibições
- Última mensagem por Lobato
Sex Fev 04, 2011 22:17
Matemática Financeira
-
- Integral equivalente - Está correto?
por Cleyson007 » Qua Abr 18, 2012 16:07
- 1 Respostas
- 1486 Exibições
- Última mensagem por DanielFerreira
Qua Abr 18, 2012 20:54
Cálculo: Limites, Derivadas e Integrais
-
- Valor nominal e taxa de juros equivalente
por gilzinha » Dom Jan 23, 2011 10:59
- 0 Respostas
- 1501 Exibições
- Última mensagem por gilzinha
Dom Jan 23, 2011 10:59
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}")
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png "{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}")
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:
Então pense o seguinte: a fração geratriz de 0,05 é
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png "{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}")
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,
da seguinte forma:
.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
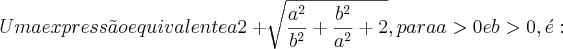
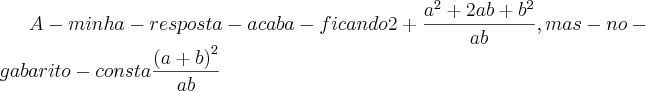
![2 + \sqrt[]{\frac{{a}^{2}}{{b}^{2}}+\frac{{b}^{2}}{{a}^{2}}+2}](/latexrender/pictures/b95dcbbd3d7fb01ec4650210983401bd.png "2 + \sqrt[]{\frac{{a}^{2}}{{b}^{2}}+\frac{{b}^{2}}{{a}^{2}}+2}")
![2 + \sqrt[]{\frac{{a}^{4} + b^4 + 2a^2b^2}{a^2{b}^{2}}}](/latexrender/pictures/53d21efb35a50349b359ba76aa6addb9.png "2 + \sqrt[]{\frac{{a}^{4} + b^4 + 2a^2b^2}{a^2{b}^{2}}}")
![2 + \sqrt[]{\frac{{a}^{4} + 2a^2b^2 + b^4}{a^2{b}^{2}}}](/latexrender/pictures/42f88c89e850647e634b13e849945c16.png "2 + \sqrt[]{\frac{{a}^{4} + 2a^2b^2 + b^4}{a^2{b}^{2}}}")
![2 + \sqrt[]{\frac{({a}^{2} + b^2)^2}{a^2{b}^{2}}}](/latexrender/pictures/6e5cfc72db84df8b0b8455f56fbe46ce.png "2 + \sqrt[]{\frac{({a}^{2} + b^2)^2}{a^2{b}^{2}}}")
