-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Mar 28, 2008 19:32
por admin » Sex Mar 28, 2008 19:32
Olá Ananda, boa noite!
De fato, a função inversa que você obteve está correta.
Mas, nem é necessário obtê-la se você utilizar uma propriedade da função inversa (que pode ser provada):
Os gráficos cartesianos de

e

são simétricos em relação à bissetriz dos quadrantes 1 e 3 do plano cartesiano.
Primeiro, pense sobre esta propriedade e tente utilizá-la na resolução.
Outras dicas para suas reflexões:
1) atualize os estudos sobre domínio e imagem de uma função e sua inversa.
2) Considere um caso mais simples. Desenhe os gráficos da parábola

e sua função inversa.
Calcule e observe o ponto comum. Relacione com a propriedade citada.
Bons estudos! Vamos conversando...
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Sex Mar 28, 2008 19:48
por Ananda » Sex Mar 28, 2008 19:48
Hmmm...
Bom, pensei nisso da simetria dos gráficos sim, mas depois de vê-los em um programa. Vi que o ponto de intersecção é no primeiro quadrante.
Ah sim, sei que o domínio da função é o contradomínio da inversa, e vice-versa!
Mas mesmo com essas informações, ainda não consegui encontrar minha "luz" no exercício!
Mas bem, farei o que me falaste e amanhã te digo o obtido!
Grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Mar 28, 2008 19:58
por admin » Sex Mar 28, 2008 19:58
OK, a dica 1 foi apenas com o intuito de revisar.
Eu não comentei intencionalmente um pequeno detalhe que resolve o problema, mas você vai perceber como conseqüência da propriedade. Acho que será sua "luz".
Até amanhã!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Ananda » Sex Mar 28, 2008 21:03
por Ananda » Sex Mar 28, 2008 21:03
Eu consegui!
Ai que felicidade! rs
Como o domínio de uma é a imagem da outra, na interseção f(x) será igual a x!
Grata!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por Ananda » Sex Mar 28, 2008 21:06
por Ananda » Sex Mar 28, 2008 21:06
Ah, e daí só considero a possibilidade positiva, porque não há raiz quadrada negativa!
Daí só resta o primeiro quadrante!
Ananda
-
Ananda
- Usuário Parceiro

-
- Mensagens: 55
- Registrado em: Sex Fev 22, 2008 19:37
- Área/Curso: Estudante
- Andamento: cursando
 por admin » Sex Mar 28, 2008 21:25
por admin » Sex Mar 28, 2008 21:25
Que ótimo, eu também fico feliz!
A propriedade diz, em outras palavras, que o eixo de simetria entre uma função e sua inversa é a reta

.
Ou seja, como as funções são simétricas, um ponto em comum estará necessariamente sobre a bissetriz

.
Até mais.
Bom final de semana!
-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
Voltar para Funções
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função quadratica
por Aline » Qui Jun 18, 2009 14:22
- 2 Respostas
- 2621 Exibições
- Última mensagem por Cleyson007

Sex Jun 19, 2009 10:00
Funções
-
- Função Quadratica
por Aline » Qui Jun 18, 2009 14:37
- 1 Respostas
- 2006 Exibições
- Última mensagem por Marcampucio

Qui Jun 18, 2009 16:45
Funções
-
- Função Quadratica
por Aline » Sáb Jun 20, 2009 18:23
- 1 Respostas
- 2082 Exibições
- Última mensagem por Molina

Dom Jun 21, 2009 20:28
Funções
-
- Função Quadratica
 por guijermous » Sáb Abr 10, 2010 10:02
por guijermous » Sáb Abr 10, 2010 10:02
- 4 Respostas
- 8026 Exibições
- Última mensagem por Molina

Sáb Abr 10, 2010 16:27
Funções
-
- Função Quadrática
por geriane » Seg Abr 12, 2010 16:14
- 0 Respostas
- 1325 Exibições
- Última mensagem por geriane

Seg Abr 12, 2010 16:14
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 definida por
definida por 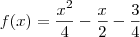 e sua inversa
e sua inversa  .
. ![f^{-1}(x)=1+2\,\sqrt[]{1+x} f^{-1}(x)=1+2\,\sqrt[]{1+x}](/latexrender/pictures/df79a0f240f347ce697636b8f9342ed6.png)
![x^2-2x-3=4(2\,\sqrt[]{1+x}) x^2-2x-3=4(2\,\sqrt[]{1+x})](/latexrender/pictures/937416660af8970b546849fb3406f141.png)
![(3+2\,\sqrt[]{3}\,;\, 3+2\,\sqrt[]{3}) (3+2\,\sqrt[]{3}\,;\, 3+2\,\sqrt[]{3})](/latexrender/pictures/b28d4b6e8be5fe9cef452c287bcd928f.png)


 e
e  e sua função inversa.
e sua função inversa.
 .
.




