Olá galera, estou com dúvida na seguinte questão, fiz a materia ja tem mais de 2 anos e nao lembro bem como resolver, consegui fazer o óbvio que é igualar o produto escalar dos vetores normais dos planos a zero, porém nao fui muito além disso. Aqui está a questão:
Determinar os valores de a e b de modo que os planos
PI1: ax+by+4z -1 =0
PI2: 3x-5y-2z+5 =0
sejam perperdiculares
Me parece ser algo bem simples, porém nao estou enxergando.
Grato pela atenção


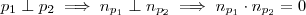 .Onde :
.Onde :  e
e 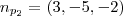 são ,respectivamente ,vetores ortogonais aos planos
são ,respectivamente ,vetores ortogonais aos planos  e
e 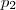 . Através da equação
. Através da equação  ,obtemos
,obtemos  isto nos faz pensar que
isto nos faz pensar que  é um número arbitrário . Mas ,tomando-se arbitrariamente dois pontos que pertencem ao plano
é um número arbitrário . Mas ,tomando-se arbitrariamente dois pontos que pertencem ao plano  .Por exemplo , fazendo-se
.Por exemplo , fazendo-se 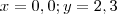 na equação no plano
na equação no plano  . Assim ,
. Assim , 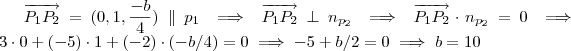 .
. 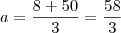 .
.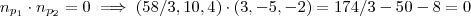 . (OK!!)
. (OK!!) . Suponha que
. Suponha que  são pontos genéricos do plano
são pontos genéricos do plano  tal que
tal que 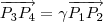 .
.  .
. 