\left\{\begin{array}
\frac{dy}{dx}
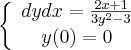
OBS: O correto é dy/dx, não conseguir inserir no LateX corretamente.
1º passo: Multipliquei cruzado a equação.

2º passo: Integrei ambos os lados
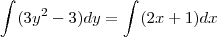
Obtive

Para encontrar a solução do PVI eu substituo 0 no y e x? Ou só no y?
b) Determine o intervalo de validade de solução.
Gostaria de uma explicação melhor sobre essa letra, pois não sei o que fazer.
c) Determine os pontos onde a solução tem um máximo local
d) Faça um esboço do gráfico


 e
e  , então :
, então :

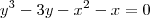
 :
: é continua no R^2 exceto nas linhas horizontais
é continua no R^2 exceto nas linhas horizontais 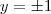 e a sua derivada em relação a y :
e a sua derivada em relação a y : 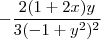 tbm é continua no R^2 exceto nas linhas horizontais
tbm é continua no R^2 exceto nas linhas horizontais