Resolva, no intervalo
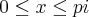 , a inequação
, a inequação  .
.Tentei resolver da seguinte maneira (que nem sei se estou no caminho certo
 ):
):
Transformei cos(2x) em produto:
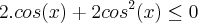
![2.cos(x) . [1 + cos(x)] \leq 0 2.cos(x) . [1 + cos(x)] \leq 0](/latexrender/pictures/f36f3bd9d0d22064894b2486b3613700.png)
Cheguei nessa inequação produto, e tentei fazer o procedimento igual numa inequação produto comum (transformar cada fator em função, achar as raízes e '"jogar" as raízes na reta pra fazer o jogo de sinais)
A raíz de 2cos(x)=0 é x=pi/2 e a raíz de 1 + cos(x) = 0 é x= pi
Mas na hora de colocar na reta me confundi.
Como que faço esse trem?

Resposta:
 {
{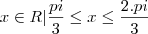 }
}

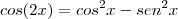 . Assim:
. Assim:
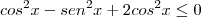

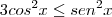




![tg(x)\geq \sqrt[]{3} tg(x)\geq \sqrt[]{3}](/latexrender/pictures/6ccd31622e44e5215b22317b513a5165.png) tem como solução
tem como solução  ou
ou 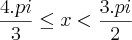 .
.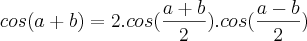


 ela não está definida, como você salientou. Mas observe que este ponto é uma solução da inequação. Volto a fazer contato em breve.
ela não está definida, como você salientou. Mas observe que este ponto é uma solução da inequação. Volto a fazer contato em breve.

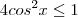

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)