 por erickm93 » Qua Mai 22, 2013 10:48
por erickm93 » Qua Mai 22, 2013 10:48
Olá, recentemente tive uma prova de Cálculo I e me surgiu uma duvida sobre a seguinte questão
Calcular o limite seguinte, utilizando o teorema do confronto, e provar sua existência através dos limites laterais, segue o limite:
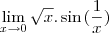
Utilizei o Wolfram Alpha para calcular este limite e ele me voltou a resposta como sendo 0, só que, minha professora corrigiu a prova e disse que este limite não existe. Minha dúvida é, qual das duas respostas está correta?
Obrigado desde já.
-
erickm93
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 22, 2013 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Física
- Andamento: cursando
 por Man Utd » Qua Mai 22, 2013 12:21
por Man Utd » Qua Mai 22, 2013 12:21
na minha opinião
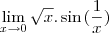
, existe sim, pois pelo teorema do confronto e lembrando que a função seno é limitada em -1 e 1.

porém
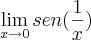
não existe pois a função oscila,veja que limites laterais diferem muito:
x=0,00000001----------f(x)=sen(1/x)=-0,98...
x=0.00000002----------f(x)=sen(1/x)=-0,64...
x=0.00000003----------f(x)=sen(1/x)=-0,54...
x=0.00000004----------f(x)=sen(1/x)=0,34
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por LuizAquino » Qua Mai 22, 2013 20:27
por LuizAquino » Qua Mai 22, 2013 20:27
erickm93 escreveu:Olá, recentemente tive uma prova de Cálculo I e me surgiu uma duvida sobre a seguinte questão
Calcular o limite seguinte, utilizando o teorema do confronto, e provar sua existência através dos limites laterais, segue o limite:
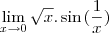
Utilizei o Wolfram Alpha para calcular este limite e ele me voltou a resposta como sendo 0, só que, minha professora corrigiu a prova e disse que este limite não existe. Minha dúvida é, qual das duas respostas está correta?
Obrigado desde já.
Man Utd escreveu:na minha opinião
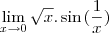
, existe sim, pois pelo teorema do confronto e lembrando que a função seno é limitada em -1 e 1.

porém
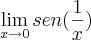
não existe pois a função oscila,veja que limites laterais diferem muito:
x=0,00000001----------f(x)=sen(1/x)=-0,98...
x=0.00000002----------f(x)=sen(1/x)=-0,64...
x=0.00000003----------f(x)=sen(1/x)=-0,54...
x=0.00000004----------f(x)=sen(1/x)=0,34
Existe um motivo muito simples para este limite
não existir: o limite lateral esquerdo não está definido.
Notem que no termo

não podemos ter

, já que no conjunto dos números reais não temos a raiz quadrada de um número
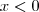
(e vale lembrar que estamos tratando em Cálculo I apenas de funções reais).
Quando o referido programa calculou este limite, ele na verdade apenas considerou o limite lateral direito. Ou seja, na verdade ele calculou:
 Observação
ObservaçãoEste exercício é interessante para ilustrar que não se pode acreditar cegamente em um programa de computador. A pessoa que está usando o programa deve fazer uma interpretação dos dados para avaliar se a resposta fornecida é coerente.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por erickm93 » Qua Mai 22, 2013 23:49
por erickm93 » Qua Mai 22, 2013 23:49
Obtive uma resposta de um colega que também achei interessante, ele me disse que o Wolfram calcula limites no conjunto dos complexos, por isso quando o mandei calcular aquele limite ele me retornou a resposta 0.
Agora com a sua resposta de que em Calculo I trabalhamos somente no conjunto dos reais, ficou ainda mais claro em minha mente a resposta para a dúvida que havia me surgido.
Agradeço pela atenção, abraços e até a próxima.
-
erickm93
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Mai 22, 2013 10:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Física
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- LIMITES - Teorema do confronto
por paola-carneiro » Dom Jun 03, 2012 20:53
- 1 Respostas
- 1903 Exibições
- Última mensagem por Fabio Wanderley

Seg Jun 04, 2012 02:45
Cálculo: Limites, Derivadas e Integrais
-
- [Questão] Teorema do Confronto dos Limites
por elisafrombrazil » Sáb Jan 21, 2017 10:45
- 1 Respostas
- 4548 Exibições
- Última mensagem por e8group

Qua Fev 01, 2017 17:14
Cálculo: Limites, Derivadas e Integrais
-
- [limite]teorema do confronto
por gabriel feron » Dom Mai 06, 2012 20:25
- 1 Respostas
- 1813 Exibições
- Última mensagem por MarceloFantini

Dom Mai 06, 2012 22:53
Cálculo: Limites, Derivadas e Integrais
-
- [Resolução de limite] Teorema do Confronto
por nievag » Ter Mai 13, 2014 00:58
- 1 Respostas
- 2126 Exibições
- Última mensagem por e8group

Ter Mai 13, 2014 10:50
Cálculo: Limites, Derivadas e Integrais
-
- [Limimite] Limite de sequência e teorema do confronto
por Aliocha Karamazov » Qui Set 15, 2011 21:01
- 5 Respostas
- 3173 Exibições
- Última mensagem por MarceloFantini

Sex Set 16, 2011 16:56
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
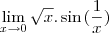



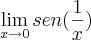 não existe pois a função oscila,veja que limites laterais diferem muito:
não existe pois a função oscila,veja que limites laterais diferem muito:
 não podemos ter
não podemos ter  , já que no conjunto dos números reais não temos a raiz quadrada de um número
, já que no conjunto dos números reais não temos a raiz quadrada de um número 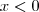 (e vale lembrar que estamos tratando em Cálculo I apenas de funções reais).
(e vale lembrar que estamos tratando em Cálculo I apenas de funções reais).

