por bakunin95 » Sex Mai 17, 2013 00:58
por bakunin95 » Sex Mai 17, 2013 00:58
Simplificando a expressão
![\frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6} \frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6}](/latexrender/pictures/b814344d1a60ea62dd48b85b84ba9cdb.png)
obtém-se o valor:
a) 27
b)
![\sqrt[5]{\frac{3}{2}} \sqrt[5]{\frac{3}{2}}](/latexrender/pictures/a722b50a444245c95d1d4fdf94fa08f6.png)
c)
![\sqrt[5]{\frac{1}{2}} \sqrt[5]{\frac{1}{2}}](/latexrender/pictures/97d791d7d42c82b4eac73e7dc7bb1264.png)
d)
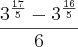
e)

usando a propriedade algébrica que mostra
![{a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}} {a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}}](/latexrender/pictures/7651b78603692599dc3046ff9f8cc005.png)
eu pensei que o resultado seria a letra d, mas o gabarito afirma que a correta é a letra A, alguém pode me explicar como chegar até esse resultado?
-
bakunin95
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mai 17, 2013 00:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Sobreira » Sex Mai 17, 2013 11:35
por Sobreira » Sex Mai 17, 2013 11:35
Amigo a expressão informada não seria essa?
![\sqrt[5]{\frac{{3}^{17}-{3}^{16}}{6}} \sqrt[5]{\frac{{3}^{17}-{3}^{16}}{6}}](/latexrender/pictures/dad5e468b3299f8e4d7aee1f7433be40.png)
Porque pela expressão fornecida anteriormente não é possível chegar a 27.
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
 por bakunin95 » Sex Mai 17, 2013 19:09
por bakunin95 » Sex Mai 17, 2013 19:09
sim, me desculpe, foi falta de atenção minha, obrigado, vc sabe como chegar na resposta?
-
bakunin95
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Mai 17, 2013 00:46
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Sobreira » Sáb Mai 18, 2013 02:26
por Sobreira » Sáb Mai 18, 2013 02:26
"The good thing about science is that it's true whether or not you believe in it."
-
Sobreira
- Colaborador Voluntário

-
- Mensagens: 122
- Registrado em: Sex Out 12, 2012 17:33
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em Questão de (EDO)
por sys_ » Sex Abr 10, 2009 19:06
- 2 Respostas
- 2323 Exibições
- Última mensagem por nakagumahissao

Seg Ago 17, 2015 13:04
Cálculo: Limites, Derivadas e Integrais
-
- Dúvida em questão de P.A.
por mushthielv » Seg Ago 17, 2009 12:18
- 3 Respostas
- 7263 Exibições
- Última mensagem por DanielFerreira

Dom Ago 23, 2009 12:59
Progressões
-
- Dúvida na questão
por GABRIELA » Ter Set 01, 2009 17:17
- 2 Respostas
- 6166 Exibições
- Última mensagem por Molina

Ter Set 01, 2009 23:28
Matrizes e Determinantes
-
- duvida na questão
por GABRIELA » Qua Set 30, 2009 17:06
- 10 Respostas
- 6670 Exibições
- Última mensagem por GABRIELA

Qua Set 30, 2009 22:42
Geometria Analítica
-
- Dúvida em uma questão
por Padoan » Qua Ago 11, 2010 18:53
- 3 Respostas
- 3220 Exibições
- Última mensagem por Padoan

Sex Ago 13, 2010 23:10
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 11 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6} \frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6}](/latexrender/pictures/b814344d1a60ea62dd48b85b84ba9cdb.png) obtém-se o valor:
obtém-se o valor:![\sqrt[5]{\frac{3}{2}} \sqrt[5]{\frac{3}{2}}](/latexrender/pictures/a722b50a444245c95d1d4fdf94fa08f6.png)
![\sqrt[5]{\frac{1}{2}} \sqrt[5]{\frac{1}{2}}](/latexrender/pictures/97d791d7d42c82b4eac73e7dc7bb1264.png)
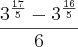

![{a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}} {a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}}](/latexrender/pictures/7651b78603692599dc3046ff9f8cc005.png) eu pensei que o resultado seria a letra d, mas o gabarito afirma que a correta é a letra A, alguém pode me explicar como chegar até esse resultado?
eu pensei que o resultado seria a letra d, mas o gabarito afirma que a correta é a letra A, alguém pode me explicar como chegar até esse resultado?
![\frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6} \frac{\sqrt[5]{{3}^{17}-{3}^{16}}}{6}](/latexrender/pictures/b814344d1a60ea62dd48b85b84ba9cdb.png) obtém-se o valor:
obtém-se o valor:![\sqrt[5]{\frac{3}{2}} \sqrt[5]{\frac{3}{2}}](/latexrender/pictures/a722b50a444245c95d1d4fdf94fa08f6.png)
![\sqrt[5]{\frac{1}{2}} \sqrt[5]{\frac{1}{2}}](/latexrender/pictures/97d791d7d42c82b4eac73e7dc7bb1264.png)
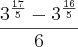

![{a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}} {a}^{\frac{k}{n}}= \sqrt[n]{{a}^{k}}](/latexrender/pictures/7651b78603692599dc3046ff9f8cc005.png) eu pensei que o resultado seria a letra d, mas o gabarito afirma que a correta é a letra A, alguém pode me explicar como chegar até esse resultado?
eu pensei que o resultado seria a letra d, mas o gabarito afirma que a correta é a letra A, alguém pode me explicar como chegar até esse resultado?
![\sqrt[5]{\frac{{3}^{17}-{3}^{16}}{6}} \sqrt[5]{\frac{{3}^{17}-{3}^{16}}{6}}](/latexrender/pictures/dad5e468b3299f8e4d7aee1f7433be40.png)


![\sqrt[5]{\frac{{3}^{15}.{3}^{2}-{3}^{15}.3}{6}} \sqrt[5]{\frac{{3}^{15}.{3}^{2}-{3}^{15}.3}{6}}](/latexrender/pictures/59496c0d9636b9e171eebdb318f61c85.png)
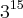 em evidência:
em evidência:![\sqrt[5]{\frac{{3}^{15}\left({3}^{2}-3 \right)}{6}} \sqrt[5]{\frac{{3}^{15}\left({3}^{2}-3 \right)}{6}}](/latexrender/pictures/5fb502c01b8f191425aa544e38b5c51b.png)
![\sqrt[5]{\frac{6.\left({3}^{15} \right)}{6}} \sqrt[5]{\frac{6.\left({3}^{15} \right)}{6}}](/latexrender/pictures/8acf800511687b33bce3725be0460c6b.png)
![\sqrt[5]{{3}^{15}} \sqrt[5]{{3}^{15}}](/latexrender/pictures/285705aa3abb28dd83731f6e02aadde0.png)
![\sqrt[5]{{3}^{5}.{3}^{5}.{3}^{5}} \sqrt[5]{{3}^{5}.{3}^{5}.{3}^{5}}](/latexrender/pictures/470bbc703b86bc5fea44a246b8f548e0.png)