


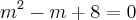
![m'=\frac{1-i\sqrt[2]{31}}{2} m'=\frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/aec8cc3dbaf056973a3220791c646e25.png) e
e ![m"=\frac{1+i\sqrt[2]{31}}{2} m"=\frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/1174083d09889b57972b4b75b312ad7a.png)
![\frac{1-i\sqrt[2]{31}}{2} \frac{1-i\sqrt[2]{31}}{2}](/latexrender/pictures/2e228b7064ec3e38b57497d953650765.png) , temos que
, temos que ![P(1)=-44-4i\sqrt[2]{31} P(1)=-44-4i\sqrt[2]{31}](/latexrender/pictures/93f5c519cf3cd15e06d12f3a37c7ad4b.png)
![\frac{1+i\sqrt[2]{31}}{2} \frac{1+i\sqrt[2]{31}}{2}](/latexrender/pictures/e071f34c73b908024dd881421ce8ae68.png) , temos que
, temos que ![P(1)=-44+4i\sqrt[2]{31} P(1)=-44+4i\sqrt[2]{31}](/latexrender/pictures/0af6eb5499176266404561d3f3ec0436.png)

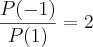
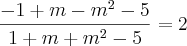
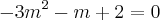

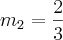
 no polinômio
no polinômio 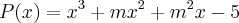 , encontrará a seguinte equação do 3º grau:
, encontrará a seguinte equação do 3º grau: 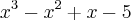 .
.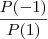 , é válida a igualdade.
, é válida a igualdade. .
.

Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)