não entendo - equação polinomial

por **natanaelskt** » Ter Mai 14, 2013 13:45

não consigo entender a seguinte equação.
não sei se estou errando,pois já conferi eu não consegui encontrar o erro.
267-) resolva,em complexos,a equação x^4-5x^2-10x-6

sabendo que duas de suas raízes são -1 e 3.

primeiro tentei o seguinte.
a soma das raizes é r1+r2+r3+r4 = 5
o produto das raizes é r1.r2.r3.r4 = -6
sendo r1=-1 e r2= 3
substituindo na equação cheguei a r3=2 e r4= 1 (ou vice versa)
o problema é que a resposta certa é -1+i e -1-i

ajuda aew galera????

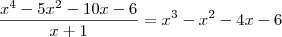
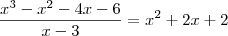
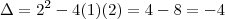
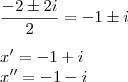
por **carlosalesouza** » Qua Mai 15, 2013 01:26

Na prática ela é muito simples...

É uma equação de grau 4, mas duas raízes já foram dadas... basta dividir a equação pelas raízes dadas (de preferência uma por vez) e vc vai obter uma equação de segundo grau...

Vamos à prova:

$\\ \frac{x^4 - 5 x^2 - 10 x -6}{x+1}=x^3 - x^2 - 4 x - 6$

Que, por sua vez:

$\\ \frac{x^3 - x^2 - 4 x - 6}{x-3}=x^2 + 2 x + 2$

Agora, aplicando Baskhara... vamos achar o Delta:
$\\ \Delta = 2^2 -4(1)(2) = 4 - 8 = -4$

Usando complexos, a raiz de -4 é 2i

Voltando ao processo:

$\\ \frac{-2 \pm 2i}{2} = -1 \pm i\\ \\ x' = -1+i\\x''=-1 - i$

Tudo certo?

É necessário tomar cuidado com alguns problemas, pois eles vem maqueados de algo mais complexos do que realmente são...

Neste caso, vc tem uma equação de segundo grau disfarçada de equação de grau 4, num exercício que exige de vc conhecimento sobre numeros complexos, equações de segundo grau e divisão de polinômios...

por **natanaelskt** » Qua Mai 15, 2013 11:06

sim,mas eu queria saber porque o método que usei deu errado.
pode me explicar?

não entendo - equação polinomial

não entendo - equação polinomial

não entendo - equação polinomial

Re: não entendo - equação polinomial

Re: não entendo - equação polinomial

Quem está online