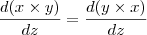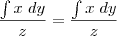por Jhenrique » Qui Mai 09, 2013 20:34
por Jhenrique » Qui Mai 09, 2013 20:34
Fala pessoal, blz!?
Dúvida: vejam este vídeo:
http://www.youtube.com/watch?v=FEnNgUfE0qM?t=2m55s. Notem que a equação diferencial,

, é solucionada integrando-se os dois membros da igualdade, assim:

. Ok...
No entanto, lembrando que a definição de integral é
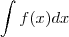
, pergunto: ao adicionar o sinal
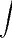
na equação, não faltou adicionar o sinal

também? Quero dizer, o

e o

da equação

não são das integrais, eles já estavam aí antes das integrais aparecerem:

. Como me explicam isto?
Obg!
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Qui Mai 09, 2013 23:06
por Russman » Qui Mai 09, 2013 23:06
Na verdade existem várias interpretações para as integrais. São somatórios, são operadores, etc...
O método de resolver as eq. df. dessa forma é um exemplo onde a integral é aplicada como operador inverso ao operador diferencial. A forma que é exposta a solução é uma forma operacional, e não formal. Seria necessário estudar melhor esse tipo de equação para deduzir-seque a sua solução pode ser tomada dessa forma. Mas acredito que a interpretação da integral como operador lhe esclarece um pouco o método, não?
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sex Mai 10, 2013 10:25
por Jhenrique » Sex Mai 10, 2013 10:25
Esclarece +/- pois isso parece implicar no seguinte... suponha a equação

, então tanto faz integrar assim
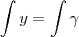
ou assim
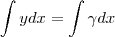
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Sex Mai 10, 2013 10:37
por Russman » Sex Mai 10, 2013 10:37
Não faz sentido aplicar a interal em funções isoladadas! Você precisa ter o diferencial de algo, pois a integral é o limite de uma soma de variações de uma dada variável. Estude a obtenção da área de curvas no plano que você vai entender o que estou dizendo.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sex Mai 10, 2013 17:11
por Jhenrique » Sex Mai 10, 2013 17:11
Tô sacando...
Outra possibilidade para a mesma equação

é dividi-la por um diferencial qualquer, assim
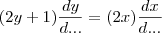
. Correto?
E se a equação fosse esta

, então acho que é possível multiplicá-la por um diferencial qualquer, assim
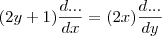
, OU aplicar o diferencial no numerador assim
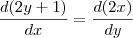
. Certo?
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
 por Russman » Sex Mai 10, 2013 22:03
por Russman » Sex Mai 10, 2013 22:03
Mas qual o intuito de dividí-la pelo diferencial? Não se esqueça que os diferenciais de y e x não são independentes, pois y é função de x. A última relação que voce escreveu não é correta. Essas manipulações dos diferenciais como se fossem variáveis algébricas só podem ser assim por uma razão bem definida...se fossem derivadas parciais a manipulação de ''passa pra um lado multiplicando e pro outro dividindo'' não funciona. Cuidado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Jhenrique » Sáb Mai 11, 2013 15:36
por Jhenrique » Sáb Mai 11, 2013 15:36
O intúito é de tomar ciência de todos os casos possíveis, de saber quais são as alternativas que esta ferramenta (ED) me fornece. Para evitar pasmos, como o do operador de integração, p ex.
Agora eu consegui enxergar que integração e derivação são operações que combinam necessariamente duas variáveis e dois operadores. O que está obscuro para mim, é saber quando a manipulação desses elementos altera a igualdade...
Por exemplo, tomando a seguinte equação

É verdade que
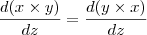
e que
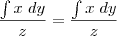
Mas não é verdade que

ou que

Fiquei confuso...
"A solução errada para o problema certo é anos-luz melhor do que a solução certa para o problema errado." - Russell Ackoff
-
Jhenrique
- Colaborador Voluntário

-
- Mensagens: 180
- Registrado em: Dom Mai 15, 2011 22:37
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Técnico em Mecânica
- Andamento: formado
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- separação de variáveis
por Thais Bomfim » Qua Dez 12, 2012 14:07
- 3 Respostas
- 2328 Exibições
- Última mensagem por Thais Bomfim

Qui Dez 13, 2012 00:22
Equações
-
- PVI- Separação de variáveis
por Crist » Sex Mar 15, 2013 21:43
- 1 Respostas
- 1707 Exibições
- Última mensagem por e8group

Sáb Mar 16, 2013 14:34
Equações Diferenciais Ordinárias e Aplicações
-
- Integral com separação de variáveis
por fernando ribeiro » Seg Nov 16, 2015 23:56
- 0 Respostas
- 1887 Exibições
- Última mensagem por fernando ribeiro

Seg Nov 16, 2015 23:56
Cálculo: Limites, Derivadas e Integrais
-
- [Achar limites de integração] Mudança de variáveis
por AlexandreTS » Sex Mar 30, 2012 18:01
- 1 Respostas
- 4927 Exibições
- Última mensagem por LuizAquino

Sex Mar 30, 2012 18:48
Cálculo: Limites, Derivadas e Integrais
-
- [Integração por Partes] Constante de integração
por KleinIll » Dom Set 01, 2019 14:11
- 2 Respostas
- 5942 Exibições
- Última mensagem por KleinIll

Sex Set 06, 2019 18:39
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 , é solucionada integrando-se os dois membros da igualdade, assim:
, é solucionada integrando-se os dois membros da igualdade, assim:  . Ok...
. Ok...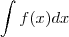 , pergunto: ao adicionar o sinal
, pergunto: ao adicionar o sinal 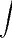 na equação, não faltou adicionar o sinal
na equação, não faltou adicionar o sinal  também? Quero dizer, o
também? Quero dizer, o  e o
e o  da equação
da equação  não são das integrais, eles já estavam aí antes das integrais aparecerem:
não são das integrais, eles já estavam aí antes das integrais aparecerem:  . Como me explicam isto?
. Como me explicam isto?

 , então tanto faz integrar assim
, então tanto faz integrar assim 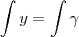 ou assim
ou assim 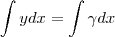
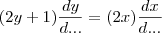 . Correto?
. Correto? , então acho que é possível multiplicá-la por um diferencial qualquer, assim
, então acho que é possível multiplicá-la por um diferencial qualquer, assim 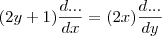 , OU aplicar o diferencial no numerador assim
, OU aplicar o diferencial no numerador assim 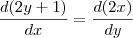 . Certo?
. Certo?