 por gilson » Ter Mai 07, 2013 21:12
por gilson » Ter Mai 07, 2013 21:12
Olá pessoal,
Estou me preparando para concurso público de nível fundamental e médio da banca CETAP em Belém PA. Espero contar com vocês!Estou na fase de resoluções de exercícios da banca já que não tem edital aberto.
Já estudei o assunto de frações, mas ainda não compreendi como resolver essa questão:
Em um órgão público, 1/3 dos funcionários tem idade entre 20 e 30 anos, 1/4 tem idade entre 30 e 40 anos e 60 funcionários têm mais de 40 anos. Quantos funcionários têm o referido órgão?
gabarito: 144
-
gilson
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 07, 2013 20:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Administração
- Andamento: cursando
 por Luis Gustavo » Ter Mai 07, 2013 21:48
por Luis Gustavo » Ter Mai 07, 2013 21:48
Entendeu tudo?
Espero ter ajudado.
Att, Luis Gustavo.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por gilson » Ter Mai 07, 2013 22:09
por gilson » Ter Mai 07, 2013 22:09
Luis Gustavo escreveu:Entendeu tudo?
Espero ter ajudado.
Att, Luis Gustavo.
Muito obrigado, acredito que a minha maior dificuldade estava em começar a questão.Valeu Luis!!!!!!!!!!!!
-
gilson
- Novo Usuário

-
- Mensagens: 9
- Registrado em: Ter Mai 07, 2013 20:31
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Administração
- Andamento: cursando
 por Luis Gustavo » Ter Mai 07, 2013 22:48
por Luis Gustavo » Ter Mai 07, 2013 22:48
gilson escreveu:Muito obrigado, acredito que a minha maior dificuldade estava em começar a questão.Valeu Luis!!!!!!!!!!!!
De nada, prazer ajudar (:
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Fração] Concurso magistério 2008
por fernandocez » Dom Jul 08, 2012 19:12
- 2 Respostas
- 2155 Exibições
- Última mensagem por fernandocez

Dom Jul 08, 2012 21:15
Álgebra Elementar
-
- raiz com fração e dizima concurso
por hevhoram » Ter Jun 24, 2014 11:50
- 3 Respostas
- 3129 Exibições
- Última mensagem por e8group

Qua Jun 25, 2014 00:25
Equações
-
- [Fração] Ajuda em problema de fração.
por smlspirit » Sex Mai 18, 2012 01:17
- 3 Respostas
- 3801 Exibições
- Última mensagem por DanielFerreira

Dom Mai 20, 2012 17:06
Álgebra Elementar
-
- fração
por leandro moraes » Qui Jan 14, 2010 19:41
- 1 Respostas
- 1691 Exibições
- Última mensagem por MarceloFantini

Qui Jan 14, 2010 20:09
Estatística
-
- Fração
por bia rosendo » Seg Jun 06, 2011 11:45
- 2 Respostas
- 4514 Exibições
- Última mensagem por Claudin

Seg Jun 06, 2011 18:34
Matemática Financeira
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 o número total de funcionários desse órgão. Temos:
o número total de funcionários desse órgão. Temos:
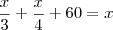
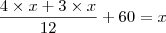
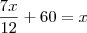
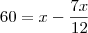
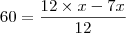
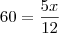
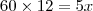

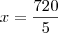
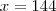

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)