 por zenildo » Ter Mai 07, 2013 17:42
por zenildo » Ter Mai 07, 2013 17:42
Se o comprimento do raio de um circulo é aumentado em 30% de seu valor, então a sua área aumenta em:
a) 60%
b)69%
c)80%
d)35%
e)45%
-
zenildo
- Colaborador Voluntário

-
- Mensagens: 309
- Registrado em: Sáb Abr 06, 2013 20:12
- Localização: SALVADOR-BA, TERRA DO AXÉ! BAÊA!!!!!
- Formação Escolar: EJA
- Área/Curso: PRETENDO/ DIREITO
- Andamento: cursando
 por Luis Gustavo » Ter Mai 07, 2013 18:58
por Luis Gustavo » Ter Mai 07, 2013 18:58
Vamos chamar as duas circunferências de

e
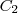
, tal que
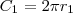
e
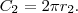
O comprimento de
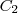
é 30% maior que o de

, ou seja, o comprimento de
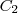
é igual a 130% do comprimento de

. Podemos escrever isso da seguinte forma:
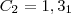
Ou ainda:
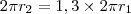
E disso decorre que:
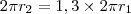
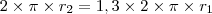
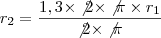
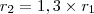
Mas tudo o que fizemos foi provar que, se o comprimento de
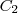
é 30% maior que o de

, o raio de
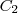
também é 30% maior que o raio de
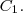
Agora amos ver qual a relação entre as áreas de

e
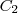
:
A área de

é igual a
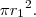
A área de
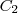
é igual a
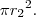
Mas como
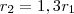
, a área de
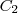
é igual a:
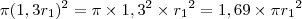
Ou seja, a área de
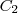
é exatamente igual a 169% da área de

, isto é, a área de
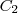
é 69% maior que a área de
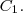 Resposta:
Resposta: b)69%.
Espero ter ajudado.
Att, Luis Gustavo.
-
Luis Gustavo
- Usuário Dedicado

-
- Mensagens: 31
- Registrado em: Seg Mai 06, 2013 15:31
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Geometria Espacial
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- geometria
por ehrefundini » Ter Abr 22, 2008 16:53
- 3 Respostas
- 7314 Exibições
- Última mensagem por admin

Qui Mai 01, 2008 15:57
Pedidos de Materiais
-
- geometria 2
por ehrefundini » Qua Mai 07, 2008 10:35
- 1 Respostas
- 6029 Exibições
- Última mensagem por admin

Qua Mai 07, 2008 10:59
Pedidos de Materiais
-
- Geometria
por rybb » Ter Ago 25, 2009 07:48
- 1 Respostas
- 2864 Exibições
- Última mensagem por Elcioschin

Seg Out 05, 2009 22:41
Trigonometria
-
- Geometria - help me?
por rybb » Ter Ago 25, 2009 07:55
- 3 Respostas
- 7312 Exibições
- Última mensagem por Molina

Qua Ago 26, 2009 23:18
Geometria
-
- geometria
por cristina » Qui Nov 19, 2009 07:05
- 0 Respostas
- 2459 Exibições
- Última mensagem por cristina

Qui Nov 19, 2009 07:05
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 0 visitantes
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



e
, tal que
e
O comprimento de
é 30% maior que o de
, ou seja, o comprimento de
é igual a 130% do comprimento de
. Podemos escrever isso da seguinte forma:
é 30% maior que o de
, o raio de
também é 30% maior que o raio de
Agora amos ver qual a relação entre as áreas de
e
:
é igual a
é igual a
Mas como
, a área de
é igual a:
é exatamente igual a 169% da área de
, isto é, a área de
é 69% maior que a área de
