 por Mell » Dom Mai 05, 2013 20:14
por Mell » Dom Mai 05, 2013 20:14
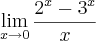
Acho que eu deveria usar o Limite fundamental
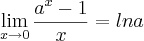
, mas não sei como aplicá-lo... :/ Alguém pode me ajudar?
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mai 05, 2013 20:21
por e8group » Dom Mai 05, 2013 20:21
No meu ponto de vista ,parece ser interessante add
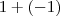
no numerador para utilizar o limite fundamental que você citou . Já tentou ?
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Mell » Dom Mai 05, 2013 21:01
por Mell » Dom Mai 05, 2013 21:01
Mas aí eu não vou estar alterando a função?? Desculpa, acho que não entendi o que você sugeriu :S
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Dom Mai 05, 2013 21:21
por e8group » Dom Mai 05, 2013 21:21
Mell escreveu:Mas aí eu não vou estar alterando a função?? Desculpa, acho que não entendi o que você sugeriu :S
Não estará alterando o resultado da função ,pois
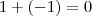
que é o elemento neutro .Assim ,
![\frac{2^x -3^x}{x} = \frac{2^x - 3^x + [1+(-1)]}{x} \frac{2^x -3^x}{x} = \frac{2^x - 3^x + [1+(-1)]}{x}](/latexrender/pictures/cd6c28e28a7e0cdb73771bd1270a8730.png)
.Por propriedade associativa (

), podemos reescrever
![\frac{2^x - 3^x + [1+(-1)]}{x} \frac{2^x - 3^x + [1+(-1)]}{x}](/latexrender/pictures/9fcde1f885869ffa9464d6dc2af29364.png)
como
![\frac{[2^x -1] +[-3^x +1]}{x} \frac{[2^x -1] +[-3^x +1]}{x}](/latexrender/pictures/14c6c67b38598008c66f7cb80ddec850.png)
e ainda

.
Agora tente concluir e comente as dúvidas .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Mell » Ter Mai 07, 2013 23:37
por Mell » Ter Mai 07, 2013 23:37
Ah sim, não tinha entendido essa parte do elemento neutro, não tenho muita facilidade com essas estratégias matemáticas... Mas agora entendi perfeitamente sua solução. Agora fica então ln 2 - ln 3, certo?? Muito obrigada!!
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Mai 08, 2013 10:15
por e8group » Qua Mai 08, 2013 10:15
De nada . O resultado do limite está correto .Para verificar a resposta digitamos " lim((2^x - 3^x)/x) as x to 0 " neste
site e pressionamos a tecla "enter" p/ exibir o resultado conforme o link abaixo :
http://www.wolframalpha.com/input/?i=li ... +as+x+to+0
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE]LIMITE FUNDAMENTAL EXPONENCIAL
por beel » Sáb Set 03, 2011 22:11
- 3 Respostas
- 2384 Exibições
- Última mensagem por beel

Dom Set 04, 2011 17:25
Cálculo: Limites, Derivadas e Integrais
-
- [Limite] Limite Exponencial
por _bruno94 » Sáb Jun 08, 2013 19:42
- 1 Respostas
- 811 Exibições
- Última mensagem por e8group

Sáb Jun 08, 2013 20:51
Cálculo: Limites, Derivadas e Integrais
-
- Limite com Exponencial
por Thyago Quimica » Qui Mai 24, 2012 17:44
- 1 Respostas
- 1048 Exibições
- Última mensagem por LuizAquino

Qui Mai 24, 2012 22:03
Cálculo: Limites, Derivadas e Integrais
-
- Limite exponencial
por Jhennyfer » Qua Mai 14, 2014 20:07
- 5 Respostas
- 2832 Exibições
- Última mensagem por e8group

Sex Mai 16, 2014 13:09
Cálculo: Limites, Derivadas e Integrais
-
- [calculo] limite - exponencial
por beel » Dom Out 30, 2011 17:51
- 4 Respostas
- 2158 Exibições
- Última mensagem por LuizAquino

Dom Out 30, 2011 19:02
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 8 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
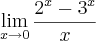
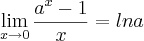 , mas não sei como aplicá-lo... :/ Alguém pode me ajudar?
, mas não sei como aplicá-lo... :/ Alguém pode me ajudar?
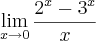
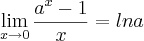 , mas não sei como aplicá-lo... :/ Alguém pode me ajudar?
, mas não sei como aplicá-lo... :/ Alguém pode me ajudar?
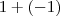 no numerador para utilizar o limite fundamental que você citou . Já tentou ?
no numerador para utilizar o limite fundamental que você citou . Já tentou ?

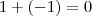 que é o elemento neutro .Assim ,
que é o elemento neutro .Assim , ![\frac{2^x -3^x}{x} = \frac{2^x - 3^x + [1+(-1)]}{x} \frac{2^x -3^x}{x} = \frac{2^x - 3^x + [1+(-1)]}{x}](/latexrender/pictures/cd6c28e28a7e0cdb73771bd1270a8730.png) .Por propriedade associativa (
.Por propriedade associativa ( ), podemos reescrever
), podemos reescrever ![\frac{2^x - 3^x + [1+(-1)]}{x} \frac{2^x - 3^x + [1+(-1)]}{x}](/latexrender/pictures/9fcde1f885869ffa9464d6dc2af29364.png) como
como ![\frac{[2^x -1] +[-3^x +1]}{x} \frac{[2^x -1] +[-3^x +1]}{x}](/latexrender/pictures/14c6c67b38598008c66f7cb80ddec850.png) e ainda
e ainda  .
.


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.