


 e razão
e razão  tem a seguinte configuração :
tem a seguinte configuração :  .
. e
e  deveremos resolver os sistema :
deveremos resolver os sistema : 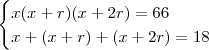 .
.

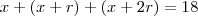 ,podemos isolar "r" ,isto é ,
,podemos isolar "r" ,isto é ,  .
. ,obtemos
,obtemos ![6x(x + 2[6-x]) = 6x(x + 12 - 2x) = 6x(-x + 12) = 66 6x(x + 2[6-x]) = 6x(x + 12 - 2x) = 6x(-x + 12) = 66](/latexrender/pictures/461f4a46d60ee51234e3e05b27508e0e.png) .Portanto ,o valor do primeiro termo da (P.A) corresponde a uma das raízes da equação do segundo grau
.Portanto ,o valor do primeiro termo da (P.A) corresponde a uma das raízes da equação do segundo grau  .Consegue terminar ?
.Consegue terminar ?

Amandatkm escreveu:pelos meus calculos deveria ficar
x(x[6+x])(x+2[6-x)=66
ao inves vc colocou 6x eu nao compreendi :S
 . Daí ,
. Daí , 
 , temos
, temos  . Então ,
. Então , ![6x(x+2r) = 66 \implies 6x(x +2[6-x]) =66 6x(x+2r) = 66 \implies 6x(x +2[6-x]) =66](/latexrender/pictures/96232eb6436c5f4b76136065386e5ee3.png) .
. Amandatkm escreveu:Tirando essa parte..quando vc chega nesse valor:
6x(-x+12)=66
ficaria assim:?
-6x²+72x-66=0
x²-12x+11=0
sim?




Amandatkm escreveu:verifiquei que vc escreveu:
6x(x+12-2x)= 6x(-x+12)=66
poderia me dizer pq o X tornou-se negativo?
 se transformar em
se transformar em  .Caso seja esta sua dúvida ,note que :
.Caso seja esta sua dúvida ,note que : ![x + 12 - 2x = [x +(-2x) ] + 12 x + 12 - 2x = [x +(-2x) ] + 12](/latexrender/pictures/6fe41f49bc30d6d769f5bcce072f7454.png) .A expressão que está dentro []é equivalente a
.A expressão que está dentro []é equivalente a  ;logo
;logo 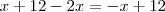 .E ,portanto
.E ,portanto 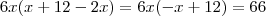 .
.xAmandatkm escreveu:no final ficaria assim
x²+12x-11=66
não consegui resolver,visto que B²-4ac não da um numero que tenha raiz :/
 ou (multiplicando todas parcelas por
ou (multiplicando todas parcelas por  ),
),  .
.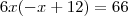 .Assim ,dividindo-se ambos membros por
.Assim ,dividindo-se ambos membros por 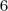 ,segue
,segue 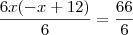
 .
. 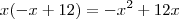 . Assim ,
. Assim , 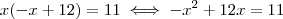 .E finalmente ,somando-se
.E finalmente ,somando-se  em ambos membros , resulta
em ambos membros , resulta 


Amandatkm escreveu:minhas raizes deram -1 e-11
eu fiz errado?
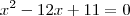 .Então :
.Então : 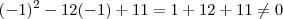 e
e 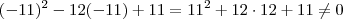 .Como podemos ver
.Como podemos ver  não é solução da equação . Infelizmente você errou o sinal das raízes .Note que :
não é solução da equação . Infelizmente você errou o sinal das raízes .Note que :  e
e 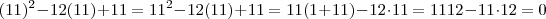 .
. Amandatkm escreveu:multipliquei a equação por -1,visto que X² nao pode ficar negativo'
 é um número positivo para qualquer
é um número positivo para qualquer  .O fato de multiplicar a equação por
.O fato de multiplicar a equação por  não irá influenciar na solução da equação muito menos em
não irá influenciar na solução da equação muito menos em  ser negativo que é um absurdo .
ser negativo que é um absurdo .


Amandatkm escreveu:iz novamente e realmente as raízes deram 1 e 11..
substitui o valor de 1 pelo R na formula de adição:
x+(x+r)+(x+2r)=18
x+x+1+x+2=18
3x=15
x=5
E realmente 5+6+7=18
porem 5*6*7 nao da 66
esta é minha duvida :/
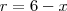 .Desta forma ,se
.Desta forma ,se  ,tem-se
,tem-se  .
. (OK!)
(OK!) (OK!)
(OK!)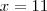 , o que acontece ?
, o que acontece ?

Amandatkm escreveu:se X for=11 R sera =-5
 .Agora você pode concluir o exercício .
.Agora você pode concluir o exercício .


Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

