 por Mell » Qua Mai 01, 2013 15:21
por Mell » Qua Mai 01, 2013 15:21
Não consigo calcular este limite:
![\lim_{x\rightarrow +\infty}\frac{\sqrt[5]{x^4+1+x}}{\sqrt[9]{x^7-x^2+3x}} \lim_{x\rightarrow +\infty}\frac{\sqrt[5]{x^4+1+x}}{\sqrt[9]{x^7-x^2+3x}}](/latexrender/pictures/7f85a54c7a330ec5bb6b653fd7577b9f.png)
Vi vários exemplos de como se calcula quando o índice da raiz e a mair potência são iguais (como x² e raiz quadrada), mas neste caso com raiz quinta e raiz nona, não sei como proceder. Acho que se não houvesse as raízes o limite daria +infinito, mas com essas raízes não sei como começar. Alguém me ajuda??
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Qua Mai 01, 2013 20:13
por e8group » Qua Mai 01, 2013 20:13
Quando o radicando é um polinômio como neste caso ,é interessante deixar o termo dominante(termo de maior grau com coeficiente não nulo de cada polinômio ) em evidência de cada polinômio .
Assim ,se

, temos :

e
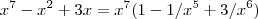
.
Todas parcelas que contém "x" no denominador ,tendem a

para

muito grande .Desta forma ,o limite a ser calculado se resume a
![\lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} \lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}}](/latexrender/pictures/3266fa0709a5fbca2fb0c645f482b4a5.png)
. Reescrevendo os radicais na forma de potência ,
![\lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} = \lim_{x\to +\infty} \frac{x^{4/5}}{x^{7/9}} = \lim_{x\to +\infty} x^{4/5 - 7/9} = \lim_{x\to +\infty} x^{1/45} = \lim_{x\to +\infty} \sqrt[45]{x} = +\infty \lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} = \lim_{x\to +\infty} \frac{x^{4/5}}{x^{7/9}} = \lim_{x\to +\infty} x^{4/5 - 7/9} = \lim_{x\to +\infty} x^{1/45} = \lim_{x\to +\infty} \sqrt[45]{x} = +\infty](/latexrender/pictures/8fe334dc278a6de08f4d4c2a316fe2a4.png)
.
OBS.:
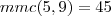
o que justifica

.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Mell » Sex Mai 03, 2013 22:45
por Mell » Sex Mai 03, 2013 22:45
Excelente!! Muito obrigada Santhiago, me ajudou muito! (:
-
Mell
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Qua Mai 01, 2013 14:48
- Localização: São Paulo, SP
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por e8group » Sáb Mai 04, 2013 02:41
por e8group » Sáb Mai 04, 2013 02:41
De nada ,não há de quê .No entanto na última linha digitei errado é
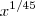
ao invés de
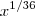
.
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [LIMITE] limites no infinito com raízes
por camila_braz » Dom Jun 11, 2017 11:42
- 0 Respostas
- 3043 Exibições
- Última mensagem por camila_braz

Dom Jun 11, 2017 11:42
Cálculo: Limites, Derivadas e Integrais
-
- [limites no infinito]Limite no infinito de um ponto finito
por moyses » Ter Ago 30, 2011 12:45
- 3 Respostas
- 3527 Exibições
- Última mensagem por LuizAquino

Ter Ago 30, 2011 18:57
Cálculo: Limites, Derivadas e Integrais
-
- [Limite no infinito] Com raizes!!
por J0elKim » Seg Abr 22, 2013 16:57
- 0 Respostas
- 1218 Exibições
- Última mensagem por J0elKim

Seg Abr 22, 2013 16:57
Cálculo: Limites, Derivadas e Integrais
-
- limites- Limite no infinito
por killerkill » Dom Ago 21, 2011 14:13
- 1 Respostas
- 1653 Exibições
- Última mensagem por LuizAquino

Dom Ago 21, 2011 20:59
Cálculo: Limites, Derivadas e Integrais
-
- [limites] limite no infinito
por baloso » Qua Abr 30, 2014 17:19
- 3 Respostas
- 2105 Exibições
- Última mensagem por Russman

Qui Mai 01, 2014 15:26
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\lim_{x\rightarrow +\infty}\frac{\sqrt[5]{x^4+1+x}}{\sqrt[9]{x^7-x^2+3x}} \lim_{x\rightarrow +\infty}\frac{\sqrt[5]{x^4+1+x}}{\sqrt[9]{x^7-x^2+3x}}](/latexrender/pictures/7f85a54c7a330ec5bb6b653fd7577b9f.png)


 , temos :
, temos :  e
e 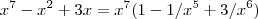 .
. para
para  muito grande .Desta forma ,o limite a ser calculado se resume a
muito grande .Desta forma ,o limite a ser calculado se resume a ![\lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} \lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}}](/latexrender/pictures/3266fa0709a5fbca2fb0c645f482b4a5.png) . Reescrevendo os radicais na forma de potência ,
. Reescrevendo os radicais na forma de potência , ![\lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} = \lim_{x\to +\infty} \frac{x^{4/5}}{x^{7/9}} = \lim_{x\to +\infty} x^{4/5 - 7/9} = \lim_{x\to +\infty} x^{1/45} = \lim_{x\to +\infty} \sqrt[45]{x} = +\infty \lim_{x\to +\infty} \frac{\sqrt[5]{x^4}}{\sqrt[9]{x^7}} = \lim_{x\to +\infty} \frac{x^{4/5}}{x^{7/9}} = \lim_{x\to +\infty} x^{4/5 - 7/9} = \lim_{x\to +\infty} x^{1/45} = \lim_{x\to +\infty} \sqrt[45]{x} = +\infty](/latexrender/pictures/8fe334dc278a6de08f4d4c2a316fe2a4.png) .
.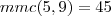 o que justifica
o que justifica  .
.
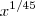 ao invés de
ao invés de 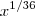 .
. .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
