 por Man Utd » Ter Abr 30, 2013 21:53
por Man Utd » Ter Abr 30, 2013 21:53
Seja ƒ uma função definida num intervalo aberto
Ie p ?
I.Suponha que

para todo x ?
I.Prove que
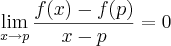
desde que o limite exista.
(Sugestão: estude os sinais de
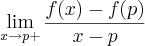
e de
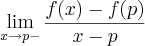
)
-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Qua Mai 01, 2013 00:38
por e8group » Qua Mai 01, 2013 00:38
Note que
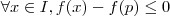
.
Daí ,
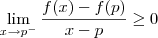
e
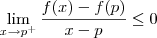
Para concluir observe que o limite existe quando os limites laterais existam e são iguais .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Man Utd » Qua Mai 01, 2013 11:43
por Man Utd » Qua Mai 01, 2013 11:43
agora entendi,então eu provo que o limite não existe já que os limites laterais diferem.
Muito Obrigado Santhiago e um bom feriado.

-
Man Utd
- Colaborador Voluntário

-
- Mensagens: 155
- Registrado em: Qua Abr 03, 2013 09:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia da Computação
- Andamento: cursando
 por e8group » Qua Mai 01, 2013 13:39
por e8group » Qua Mai 01, 2013 13:39
Para ficar mais claro ,tomemos
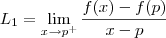
e
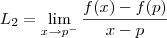
. Como
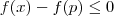
para todo

em

e
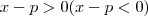
quando
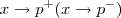
concluímos que
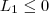
e
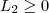
.Ou seja ,
![L_1 \in (-\infty,0] L_1 \in (-\infty,0]](/latexrender/pictures/2502ddfcf4977a451d429a3cab2bdfc2.png)
e
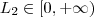
. Desde que o limite exista ,obrigatoriamente

.
Assim ,
![L_1 = L_2 \implies L_1 \in (-\infty,0] \wedge L_1\in [0,+\infty) ,L_2 \in (-\infty,0] \wedge L_2\in [0,+\infty) \iff L_1 \in (-\infty,0]\cap [0,+\infty) = \{0\} , L_2 \in (-\infty,0]\cap [0,+\infty) = \{0\} L_1 = L_2 \implies L_1 \in (-\infty,0] \wedge L_1\in [0,+\infty) ,L_2 \in (-\infty,0] \wedge L_2\in [0,+\infty) \iff L_1 \in (-\infty,0]\cap [0,+\infty) = \{0\} , L_2 \in (-\infty,0]\cap [0,+\infty) = \{0\}](/latexrender/pictures/c690ea3ccd8e2620f35ac4b8b189ed1c.png)
.
Ou seja ,
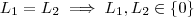
.
Daí ,
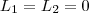
.
E portanto ,para que o limite exista, há uma única possibilidade ,ele ser igual a zero .
Obrigado ,bom feriado também .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Cálculo: Limites, Derivadas e Integrais
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Prove que o limite existe
por Cleyson007 » Sáb Abr 28, 2012 16:48
- 2 Respostas
- 1477 Exibições
- Última mensagem por MarceloFantini

Dom Abr 29, 2012 15:02
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Prove a partir da definição de limite
por Ruan Petterson » Qui Nov 28, 2013 23:13
- 6 Respostas
- 3636 Exibições
- Última mensagem por e8group

Sex Nov 29, 2013 10:05
Cálculo: Limites, Derivadas e Integrais
-
- Prove: n(A X B) = n(A) * n(B)
por juliomarcos » Dom Set 14, 2008 02:58
- 3 Respostas
- 5273 Exibições
- Última mensagem por admin

Qua Set 24, 2008 05:33
Conjuntos
-
- Prove que
por Balanar » Dom Ago 29, 2010 17:22
- 1 Respostas
- 2310 Exibições
- Última mensagem por MarceloFantini

Seg Ago 30, 2010 01:24
Álgebra Elementar
-
- Prove
por chronoss » Dom Abr 21, 2013 16:52
- 3 Respostas
- 3066 Exibições
- Última mensagem por chronoss

Seg Abr 22, 2013 14:23
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 9 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 para todo x ? I.Prove que
para todo x ? I.Prove que 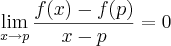 desde que o limite exista.
desde que o limite exista.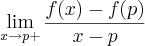 e de
e de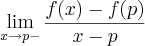 )
)
 para todo x ? I.Prove que
para todo x ? I.Prove que 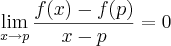 desde que o limite exista.
desde que o limite exista.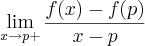 e de
e de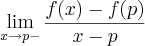 )
)
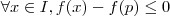 .
. 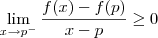
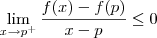



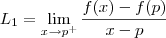 e
e 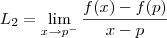 . Como
. Como 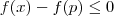 para todo
para todo  em
em  e
e 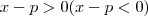 quando
quando 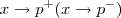 concluímos que
concluímos que 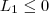 e
e 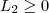 .Ou seja ,
.Ou seja , ![L_1 \in (-\infty,0] L_1 \in (-\infty,0]](/latexrender/pictures/2502ddfcf4977a451d429a3cab2bdfc2.png) e
e 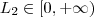 . Desde que o limite exista ,obrigatoriamente
. Desde que o limite exista ,obrigatoriamente  .
. ![L_1 = L_2 \implies L_1 \in (-\infty,0] \wedge L_1\in [0,+\infty) ,L_2 \in (-\infty,0] \wedge L_2\in [0,+\infty) \iff L_1 \in (-\infty,0]\cap [0,+\infty) = \{0\} , L_2 \in (-\infty,0]\cap [0,+\infty) = \{0\} L_1 = L_2 \implies L_1 \in (-\infty,0] \wedge L_1\in [0,+\infty) ,L_2 \in (-\infty,0] \wedge L_2\in [0,+\infty) \iff L_1 \in (-\infty,0]\cap [0,+\infty) = \{0\} , L_2 \in (-\infty,0]\cap [0,+\infty) = \{0\}](/latexrender/pictures/c690ea3ccd8e2620f35ac4b8b189ed1c.png) .
. 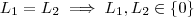 .
. 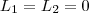 .
. 
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.